
分析 由题意可得对区间[3,4]上的每一个x的值,不等式f(x)>($\frac{1}{2}$)x+m恒成立,令h(x)=f(x)-($\frac{1}{2}$)x ,利用单调性求得h(x)的最小值,可得实数m的取值范围.
解答 解:f(x)=log${\;}_{\frac{1}{2}}$$\frac{x+1}{x-1}$=${log}_{\frac{1}{2}}(1+\frac{2}{x-1})$,∵由于$\frac{2}{x-1}$在 区间(1,+∞)内单调递减,故f(x)在[3,4]上单调递增,
则对区间[3,4]上的每一个x的值,不等式f(x)>($\frac{1}{2}$)x+m恒成立.
令h(x)=f(x)-($\frac{1}{2}$)x ,则得h(x)在[3,4]上单调递增,
故h(x)的最小值为h(3)=-1-$\frac{1}{8}$=-$\frac{9}{8}$,∴m<-$\frac{9}{8}$,
故答案为:$(-∞,-\frac{9}{8})$.
点评 本题主要考查函数的奇偶性和单调性,汗水肚饿恒成立问题,求函数的值域,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
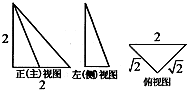
| A. | 2 | B. | $\sqrt{2}$+1 | C. | $\sqrt{2}+\sqrt{3}$+3 | D. | $\sqrt{3}$+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
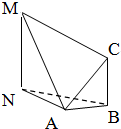 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=200m,求山高MN.
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=200m,求山高MN.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | -$\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com