
【题目】已知平面内一动点 ![]() 到点
到点 ![]() 的距离与点
的距离与点 ![]() 到 x
到 x![]() 轴的距离的差等于1.
轴的距离的差等于1.
(1)求动点 ![]() 的轨迹
的轨迹 ![]() 的方程;
的方程;
(2)过点 ![]() 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ![]() ,设
,设 ![]() 与轨迹
与轨迹 ![]() 相交于点
相交于点 ![]() ,
, ![]() 与轨迹
与轨迹 ![]() 相交于点
相交于点 ![]() ,求
,求 ![]() 的最小值.
的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,已知a=![]() c.
c.
(1)若∠A=2∠B,求cosB;
(2)若AC=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
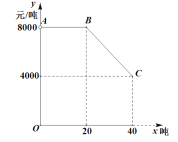
【题目】乔经理到老陈的果园里一次性采购一种水果,他俩商定:乔经理的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间函数关系的图像如图中的折线段
(吨)之间函数关系的图像如图中的折线段![]() 所示(不包含端点
所示(不包含端点![]() 但包含端点
但包含端点![]() ).
).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)已知老陈种植水果的成本是2800元/吨,那么乔经理的采购量为多少时,老陈在这次买卖中所获的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.如果平面 ![]() 平面
平面 ![]() ,则
,则 ![]() 内任意一条直线必垂直于
内任意一条直线必垂直于 ![]()
B.若直线 ![]() 不平行于平面
不平行于平面 ![]() ,则
,则 ![]() 内不存在直线平行于直线
内不存在直线平行于直线 ![]()
C.如果平面 ![]() 不垂直于平面
不垂直于平面 ![]() ,那么平面
,那么平面 ![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面 ![]()
D.若直线 ![]() 不垂直于平面
不垂直于平面 ![]() ,则
,则 ![]() 内不存在直线垂直于直线
内不存在直线垂直于直线 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥 ![]() 中,
中, ![]() 底面
底面 ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() 在
在 ![]() ,且
,且 ![]() .
.
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)在线段 ![]() 上是否存在点
上是否存在点 ![]() ,使二面角
,使二面角 ![]() 的大小为
的大小为 ![]() ?若存在,求出
?若存在,求出 ![]() 的长;
的长;
若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,点
,点 ![]() 在x轴的正半轴上,过点M的直线
在x轴的正半轴上,过点M的直线 ![]() 与抛物线C相交于A,B两点,O为坐标原点.
与抛物线C相交于A,B两点,O为坐标原点.
(1)若 ![]() ,且直线
,且直线 ![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2)是否存在定点M,使得不论直线 ![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com