Question

16．函数y=f（x）的最小正周期为2，且f（-x）=f（x）．当x∈[0，1]时f（x）=-x+1，函数y=f（x）图象对称轴方程x=k（k∈Z），在区间[-3，4]上，函数G（x）=f（x）-（$\frac{1}{2}$）^|x|的零点个数有6个．

Answer 1

分析 函数G（x）=f（x）-（$\frac{1}{2}$）^|x|的零点个数即为y=f（x）与y=（$\frac{1}{2}$）^|x|的图象的交点个数，只要由函数的性质，在同一个坐标系中作出两个函数的图象，即可的答案．

解答 解：由题意可知，函数G（x）=f（x）-（$\frac{1}{2}$）^|x|的零点个数即为y=f（x）与y=（$\frac{1}{2}$）^|x|的图象的交点个数，
函数y=f（x）周期为2，且为偶函数，函数y=（$\frac{1}{2}$）^|x|为偶函数，
在同一个坐标系中作出它们的图象，
可得对称轴方程为x=k（k∈Z），交点个数为6，
故答案是：x=k（k∈Z）；6．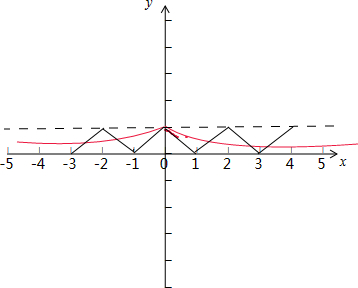

点评 本题考查由函数的性质作函数的图象，以及函数的零点问题转化成两函数图象的交点问题，同时考查了作图的能力，属中档题．