
分析 (1)连结BD,由于A+C=180°则cosA=-cosC,在△BCD中和在△ABD中,分别利用余弦定理列出方程,联立后求得BD、角C、A,利用三角形的公式求出四边形ABCD的面积;
(2)由正弦定理求出AC,在△ABC中和在△ADC中,分别利用余弦定理列出方程,化简后利用基本不等式分别求出AB+BC、AD+DC范围,即可四边形ABCD的周长的最大值.
解答 解:(1)连结BD,由于A+C=180°,则cosA=-cosC,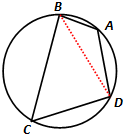
由题设及余弦定理得:
在△BCD中,BD2=BC2+CD2-2BC•CDcosC=13-12cosC,…①
在△ABD中,BD2=AB2+DA2-2AB•DAcosA=5+4cosC,…②
由①-②得,cosC=$\frac{1}{2}$,所以C=60°,则A=120°,
所以边形ABCD的面积S=S△ABD+S△BCD=$\frac{1}{2}AB•ADsinA+\frac{1}{2}BC•CDsinC$
=$\frac{1}{2}×2×4×\frac{\sqrt{3}}{2}+\frac{1}{2}×6×4×\frac{\sqrt{3}}{2}$=8$\sqrt{3}$;
(2)∵R=2,B=60°,
∴在△ABC中,由正弦定理得$\frac{AC}{sinB}=2R$,则AC=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
在△ABC中由余弦定理得,AC2=AB2+BC2-2AB•BCcosB,
则AB2+BC2-AB•BC=12,即(AB+BC)2-12=3AB•BC,
∵AB+BC≥$2\sqrt{AB•BC}$,∴AB•BC≤$\frac{(AB+BC)^{2}}{4}$,
代入上式得,(AB+BC)2-12≤$\frac{{3(AB+BC)}^{2}}{4}$,
解得AB+BC≤4$\sqrt{3}$,(当且仅当AB=BC取等号)
由于B+D=180°,则D=120°,
在△ADC中由余弦定理得,AC2=AD2+DC2-2AD•DCcosD,
则AD2+DC2+AD•DC=12,即(AD+DC)2-12=AD•DC,
∵AD+DC≥$2\sqrt{AD•DC}$,∴AD•DC≤$\frac{{(AD+DC)}^{2}}{4}$,
代入上式得,(AD+DC)2-12≤$\frac{{(AD+DC)}^{2}}{4}$,
解得AD+DC≤4,(当且仅当AD=DC取等号)
∴四边形ABCD的周长L=AB+AC+AD+CD≤4$\sqrt{3}$+4=4($\sqrt{3}+$1),
即四边形ABCD的周长的最大值是4($\sqrt{3}+1$).
点评 本题考查正弦定理和余弦定理,基本不等式的应用,以及方程思想,考查化简、变形能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3≤t≤0 | B. | -3≤t≤1 | C. | -2≤t≤0 | D. | 0≤t≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x) | B. | -f(x) | C. | -g(-x) | D. | g(-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\underset{lim}{n→∞}$(-1)n+1 | B. | $\underset{lim}{n→∞}$2n | C. | $\underset{lim}{x→{0}^{+}}$lnx | D. | $\underset{lim}{x→∞}$$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在平面α,使得a?α且b⊥α | |
| B. | 存在平面β,使得b?β 且a∥β | |
| C. | 若点A,B分别在直线a,b上,且满足AB⊥b,则一定有AB⊥a | |
| D. | 过空间某点不一定存在与直线a,b都平行的平面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com