
分析 由题意求得a6<0,a5>0,且a5>|a6|.然后逐一判断四个选项得答案.
解答 解:在等差数列{an}中,由S10>0,S11<0,
得$\frac{10({a}_{1}+{a}_{10})}{2}=5({a}_{5}+{a}_{6})>0$,$\frac{11({a}_{1}+{a}_{11})}{2}=11{a}_{6}<0$,
∴a6<0,a5>0,且a5>|a6|.
则数列{an}为递减数列,且a1>0,则(1)正确;
∵数列前5项为正,自第6项起为负,则S5最大,(2)错误;
a3>0,(3)正确;a6<0,(4)错误.
故答案为:(1),(3).
点评 本题考查等差数列的前n项和,考查了等差数列的性质,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
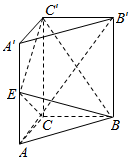 如图,直三棱柱ABC-A′B′C′中,AA′=2AC=2BC,E为AA′的中点,C′E⊥BE.
如图,直三棱柱ABC-A′B′C′中,AA′=2AC=2BC,E为AA′的中点,C′E⊥BE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com