
���� ���������������������������ʾ�Ͷ����ǵ����ң����ҹ�ʽ���Լ����Dz�����ҹ�ʽ����������ǵĺ���ֵ�����ɵõ�������㣻
����������ɵ�$\frac{��}{3}$��B���У��������Һ�����ͼ������ʣ��ɵ�f��B������ֵ�����ɵõ�����Χ��
��� �⣺��������$\overrightarrow{m}$=��cos$\frac{x}{2}$��-1����$\overrightarrow{n}$=��$\sqrt{3}$sin$\frac{x}{2}$��cos2$\frac{x}{2}$����
�ɵú���f��x��=$\overrightarrow{m}$•$\overrightarrow{n}$=$\sqrt{3}$sin$\frac{x}{2}$cos$\frac{x}{2}$-cos2$\frac{x}{2}$=$\frac{\sqrt{3}}{2}$sinx-$\frac{1+cosx}{2}$
=sin��x-$\frac{��}{6}$��-$\frac{1}{2}$��
��f��x��=0���ɵ�sin��x-$\frac{��}{6}$��=$\frac{1}{2}$��
��x-$\frac{��}{6}$=2k��+$\frac{��}{6}$��2k��+$\frac{5��}{6}$��k��Z��
��Ϊx=2k��+$\frac{��}{3}$��2k��+�У�k��Z��
��x��[0����]���ɵ�f��x�������Ϊ$\frac{��}{3}$��
����A=$\frac{��}{3}$��B�ǡ�ABC�е�����ڽǣ�
��ΪB��$\frac{��}{3}$��B�ݦ�-$\frac{��}{3}$-B�����$\frac{��}{3}$��B���У�
��f��B��=sin��B-$\frac{��}{6}$��-$\frac{1}{2}$��
��$\frac{��}{6}$��B-$\frac{��}{6}$��$\frac{5��}{6}$���ɵ�$\frac{1}{2}$��sin��B-$\frac{��}{6}$����1��
��Ϊ0��f��B����$\frac{1}{2}$��
��f��B����ȡֵ��Χ��[0��$\frac{1}{2}$]��
���� ���⿼���������������������ʾ���Լ������ǹ�ʽ�����Dz�����ҹ�ʽ���������Һ�����ͼ������ʣ��������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
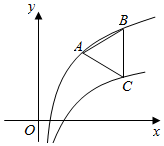 ��ͼ����A��B�ں���y=log2x+2��ͼ���ϣ���C�ں���y=log2x��ͼ���ϣ�����ABCΪ�ȱ������Σ���ֱ��BC��y�ᣬ���A������Ϊ��m��n������m=��������
��ͼ����A��B�ں���y=log2x+2��ͼ���ϣ���C�ں���y=log2x��ͼ���ϣ�����ABCΪ�ȱ������Σ���ֱ��BC��y�ᣬ���A������Ϊ��m��n������m=��������| A�� | 2 | B�� | 3 | C�� | $\sqrt{2}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -7 | B�� | 7 | C�� | -28 | D�� | 28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{7}$ | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com