
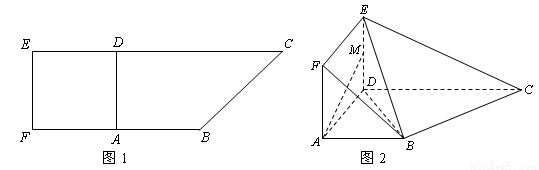
如图1,在直角梯形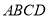 中,
中,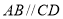 ,
,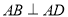 ,且
,且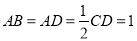 .现以
.现以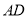 为一边向形外作正方形
为一边向形外作正方形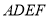 ,然后沿边
,然后沿边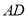 将正方形
将正方形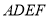 翻折,使平面
翻折,使平面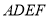 与平面
与平面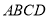 垂直,
垂直,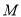 为
为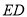 的中点,如图2.
的中点,如图2.
(1)求证: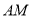 ∥平面
∥平面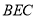 ;
;
(2)求证: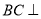 平面
平面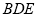 ;
;
(3)求点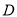 到平面
到平面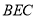 的距离.
的距离.
(1)见解析(2)见解析(3)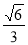
【解析】
试题分析:(1)取EC的中点为N,则MN平行且等于CD的一半,由AB平行且等于CD的一半及平行公理知,NM平行且等于AB,所以ABNM是平行四边形,所以AM平行BN,所以AM平行面BEC;(2)由面ADEF⊥面ADCB及DE⊥AD,面面垂直性质定理知,DE⊥面ADCB,所以AD⊥BC,通过计算及勾股定理可知DB⊥BC,由线面垂直的判定定理可得BC垂直面DBE;(3)先算出三棱锥E-DBC的体积及三角形EBC的面积,再利用三棱锥E-DCB的体积与三棱锥D-EBC的体积相等即可求出点D到面BEC的距离.
试题解析:(1)证明:取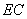 中点
中点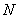 ,连结
,连结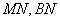 .
.
在△ 中,
中,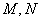 分别为
分别为 的中点,
的中点,
所以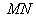 ∥
∥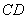 ,且
,且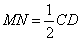 .
.
由已知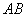 ∥
∥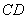 ,
,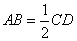 ,
,
所以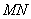 ∥
∥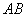 ,且
,且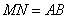 . 3分
. 3分
所以四边形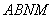 为平行四边形.
为平行四边形.
所以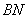 ∥
∥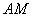 . 4分
. 4分
又因为 平面
平面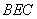 ,且
,且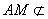 平面
平面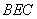 ,
,
所以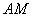 ∥平面
∥平面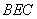 . 4分
. 4分
(2)证明:在正方形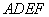 中,
中,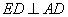 .
.
又因为平面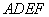
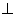 平面
平面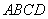 ,且平面
,且平面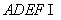 平面
平面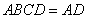 ,
,
所以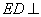 平面
平面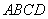 .
.
所以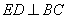 . 6分
. 6分
在直角梯形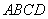 中,
中,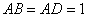 ,
,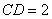 ,可得
,可得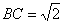 .
.
在△ 中,
中,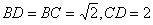 ,
, 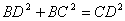 .
.
所以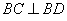 .
.
所以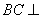 平面
平面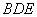 . 8分
. 8分
(3)由(2)知,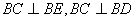
所以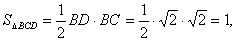 又因为
又因为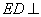 平面
平面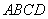
又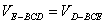 =
= 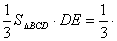 10分
10分
所以,D到面BEC的距离为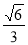 12分
12分
考点:空间线面平行的判定与性质,空间面面垂直性质定理,线面垂直的判定与性质,三棱锥的体积公式,转化思想,空间想象能力,推理论证能力


科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知椭圆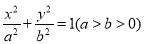 的离心率为
的离心率为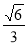 .
.
(1)若原点到直线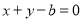 的距离为
的距离为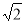 ,求椭圆的方程;
,求椭圆的方程;
(2)设过椭圆的右焦点且倾斜角为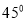 的直线和椭圆交于A,B两点.
的直线和椭圆交于A,B两点.
当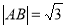 ,求b的值;
,求b的值;
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
函数 的图像( ).
的图像( ).
A、 关于原点对称 B、关于主线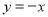 对称
对称
C、 关于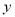 轴对称 D、关于直线
轴对称 D、关于直线 对称
对称
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则 =( )
=( )
A.- B.-
B.-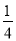 C.
C.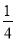 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:填空题
在平面直角坐标系xoy中,若直线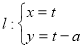 (t为参数)过椭圆C:
(t为参数)过椭圆C: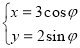 (
(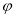 为参数)的右顶点,则常数a的值为______.
为参数)的右顶点,则常数a的值为______.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设函数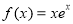 ,则( )
,则( )
A.x=1为 的极大值点
的极大值点
B. x=-1为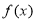 的极大值点
的极大值点
C.x=1为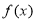 的极小值点
的极小值点
D. x=-1为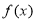 的极小值点
的极小值点
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末理科数学试卷(解析版) 题型:选择题
现有四个函数:①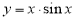 ;②
;② ;③
;③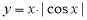 ;④
;④ 的图象(部分)如下:
的图象(部分)如下:

则按照从左到右图象对应的函数序号安排正确的一组是
A.①④②③ B.①④③② C.④①②③ D.③④②①
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江大庆铁人中学高二下学期四月月考理科数学试卷(解析版) 题型:填空题
若随机变量X的概率分布密度函数是 (x∈R),则 E(2X1)=_________.
(x∈R),则 E(2X1)=_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com