
分析 (1)求出函数f(x)的分段函数的形式,通过讨论x的范围得到关于x的不等式组,解出取并集即可;
(2)x<-$\frac{3}{2}$时,f(x)=-3x-2>$\frac{5}{2}$,问题转化为a+1≤$\frac{5}{2}$,求出a的范围即可.
解答 解:(1)∵f(x)=|2x+3|+|x-1|,
∴f(x)=$\left\{\begin{array}{l}{-3x-2,x<-\frac{3}{2}}\\{x+4,-\frac{3}{2}≤x≤1}\\{3x+2,x>1}\end{array}\right.$,
f(x)>4?$\left\{\begin{array}{l}{x<-\frac{3}{2}}\\{-3x-2>4}\end{array}\right.$或$\left\{\begin{array}{l}{-\frac{3}{2}≤x≤1}\\{x+4>4}\end{array}\right.$或$\left\{\begin{array}{l}{x>1}\\{3x+2>4}\end{array}\right.$
?x<-2或0<x≤1或x>1,
综上,不等式f(x)>4的解集是:(-∞,-2)∪(0,+∞);
(2)由(1)得:x<-$\frac{3}{2}$时,f(x)=-3x-2,
∵x<-$\frac{3}{2}$时,f(x)=-3x-2>$\frac{5}{2}$,
∴a+1≤$\frac{5}{2}$,解得:a≤$\frac{3}{2}$,
∴实数a的范围是(-∞,$\frac{3}{2}$].
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{13}$ | B. | -$\frac{4}{13}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
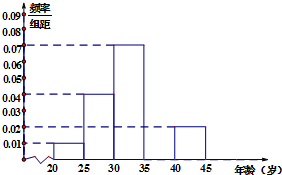 当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:
当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:| 组数 | 分组(单位:岁) | 频数 | 频率 |
| 1 | [20,25) | 5 | 0.05 |
| 2 | [25,30) | 20 | 0.20 |
| 3 | [30,35) | a | 0.35 |
| 4 | [35,40) | 30 | b |
| 5 | [40,45] | 10 | 0.10 |
| 合计 | n | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
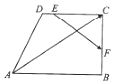 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=3,BC=DC=2,若E,F分别是线段DC和BC上的动点,则$\overrightarrow{AC}•\overrightarrow{EF}$的取值范围是[-4,6].
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=3,BC=DC=2,若E,F分别是线段DC和BC上的动点,则$\overrightarrow{AC}•\overrightarrow{EF}$的取值范围是[-4,6].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 两条相交直线 | C. | 球面 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com