
���� ��1���������ַ��̵�ת��������������ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
��2��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-1-\frac{\sqrt{2}}{2}m}\\{y=\frac{\sqrt{2}}{2}m}\end{array}\right.$��mΪ��������������Բ���̣������ɵ�7m2+6$\sqrt{2}$m-18=0�����ò����ļ������壬�ɵý��ۣ�
��� �⣺��1��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-1-t}\\{y=t}\end{array}\right.$��tΪ����������ͨ����Ϊx+y+1=0��
����C�ļ����귽��Ϊ��2��3+sin2�ȣ�=12��ֱ�����귽��Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1��
��2��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-1-\frac{\sqrt{2}}{2}m}\\{y=\frac{\sqrt{2}}{2}m}\end{array}\right.$��mΪ��������������Բ���̣������ɵ�7m2+6$\sqrt{2}$m-18=0��
��A��B��Ӧ�IJ���Ϊm1��m2����m1+m2=-$\frac{6\sqrt{2}}{7}$��m1m2=-$\frac{18}{7}$��
��M��Ӧ�IJ���Ϊ-$\frac{3\sqrt{2}}{7}$����M��-$\frac{4}{7}$��$\frac{3}{7}$����
��N��-1��0������|MN|=$\frac{3\sqrt{2}}{7}$
��|AN|-|BN|+|MN|+|AN|•|BN|=$\sqrt{\frac{72}{49}+\frac{72}{7}}$+$\frac{3\sqrt{2}}{7}$+$\frac{18}{7}$=6+$\frac{3\sqrt{2}}{7}$��
���� ���⿼�����ַ��̵�ת��������������̵����ã������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
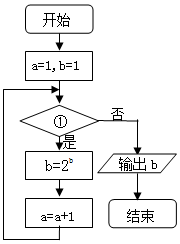
| A�� | a��3�� | B�� | a��3�� | C�� | a��3�� | D�� | a��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
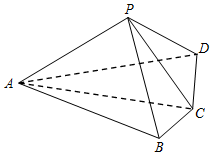 ��ͼ������P-ABCD�У�ƽ��PAC��ƽ��ABCD��AC=2BC=2CD=4����ACB=��ACD=60�㣮
��ͼ������P-ABCD�У�ƽ��PAC��ƽ��ABCD��AC=2BC=2CD=4����ACB=��ACD=60�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com