
分析 由正弦定理可求c=2sinC,a=2sinA,设周长为y,利用三角函数恒等变换的应用化简得y=4sin(A+$\frac{π}{6}$)+2,可求范围$\frac{π}{6}$<A+$\frac{π}{6}$<$\frac{5π}{6}$,利用正弦函数的性质可求取值范围.
解答 解:∵$\frac{c}{sinC}=\frac{a}{sinA}=\frac{b}{sinB}=\frac{2}{\frac{\sqrt{3}}{2}}=\frac{4\sqrt{3}}{3}$,
∴c=$\frac{4\sqrt{3}}{3}$sinC,a=$\frac{4\sqrt{3}}{3}$sinA,----(7分)
设周长为y,则y=a+c+b=$\frac{4\sqrt{3}}{3}$sinA+$\frac{4\sqrt{3}}{3}$sinC+2
=$\frac{4\sqrt{3}}{3}$sinA+$\frac{4\sqrt{3}}{3}$sin($\frac{2π}{3}$-A)+2
=2$\sqrt{3}$sinA+2cosA+2,----(8分)
=4sin(A+$\frac{π}{6}$)+2,-------(9分)
∵0<A<$\frac{2π}{3}$,
∴$\frac{π}{6}$<A+$\frac{π}{6}$<$\frac{5π}{6}$,
∴$\frac{1}{2}$<sin(A+$\frac{π}{6}$)≤1,
∴y=4sin(A+$\frac{π}{6}$)+2∈(4,6].
∴周长的取值范围是(4,6].-------(12分)
点评 本题主要考查了正弦定理,余弦定理,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的应用,考查了转化思想,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三10月月考数学(文)试卷(解析版) 题型:选择题
已知抛物线 的焦点到双曲线
的焦点到双曲线 的渐近线的距离不大于
的渐近线的距离不大于 ,则双曲线
,则双曲线 的离心率的取值范围是( )
的离心率的取值范围是( )
A. B.
B.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:解答题
如图,四棱锥 的底面
的底面 是矩形,平面
是矩形,平面 平面
平面 ,
,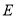 是
是 的中点,且
的中点,且 ,
, .
.

(1)求证: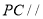 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | 5 | C. | $\sqrt{31}$ | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {-3,-1,0} | C. | {-1,0,2} | D. | {-3,0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com