
分析 (1)分两种情况进行研究,当0<x<80时,投入成本为C(x)=$\frac{1}{3}$x2+10x(万元),根据年利润=销售收入-成本,列出函数关系式,当x≥80时,投入成本为C(x)=51x+$\frac{10000}{x}$-1450,根据年利润=销售收入-成本,列出函数关系式,最后写成分段函数的形式,从而得到答案;
(2)根据年利润的解析式,分段研究函数的最值,当0<x<80时,利用二次函数求最值,当x≥80时,利用基本不等式求最值,最后比较两个最值,即可得到答案.
解答 解:(1)∵每件商品售价为0.05万元,
∴x千件商品销售额为0.05×1000x万元,
①当0<x<80时,根据年利润=销售收入-成本,
∴L(x)=(0.05×1000x)-$\frac{1}{3}$x2-10x-250=-$\frac{1}{3}$x2+40x-250;
②当x≥80时,根据年利润=销售收入-成本,
∴L(x)=(0.05×1000x)-51x-$\frac{10000}{x}$+1450-250=1200-(x+$\frac{10000}{x}$).
综合①②可得,L(x)=$\left\{\begin{array}{l}{\frac{1}{3}{x}^{2}+40x-250,0<x<80}\\{1200-(x+\frac{10000}{x}),x≥80}\end{array}\right.$;
(2)①当0<x<80时,L(x)=-$\frac{1}{3}$x2+40x-250=-$\frac{1}{3}$(x-60)2+950,
∴当x=60时,L(x)取得最大值L(60)=950万元;
②当x≥80时,L(x)=1200-(x+$\frac{10000}{x}$)≤1200-2$\sqrt{x•\frac{10000}{x}}$=1200-200=1000,
当且仅当x=$\frac{10000}{x}$,即x=100时,L(x)取得最大值L(100)=1000万元.
综合①②,由于950<1000,
∴年产量为100千件时,该厂在这一商品的生产中所获利润最大.
点评 本题考查学生根据实际问题选择合适的函数类型的能力,以及运用基本不等式求最值的能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | M=S | B. | M∩S=∅ | C. | M∪S=S | D. | M∪S=M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 完全归纳推理,结论正确 | B. | 三段论推理,结论正确 | ||
| C. | 传递性关系推理,结论正确 | D. | 大前提正确,推理的结论错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .$\frac{1}{2}$ | B. | $\frac{4}{15}$ | C. | $\frac{2}{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系中, 以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系, 已知点
轴的非负半轴为极轴建立极坐标系, 已知点 的极坐标为
的极坐标为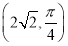 ,曲线
,曲线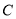 的参数方程为
的参数方程为 为参数).
为参数).
(1)直线 过
过 且与曲线
且与曲线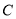 相切, 求直线
相切, 求直线 的极坐标方程;
的极坐标方程;
(2)点 与点
与点 关于
关于 轴对称, 求曲线
轴对称, 求曲线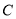 上的点到点
上的点到点 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三10月月考数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系 中,以
中,以 为极点,
为极点,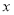 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线 极坐标方程为
极坐标方程为 ,曲线
,曲线 参数方程为
参数方程为 (
( 为参数).
为参数).
(Ⅰ)求 的直角坐标方程;
的直角坐标方程;
(Ⅱ)当 与
与 有两个公共点时,求实数
有两个公共点时,求实数 取值范围.
取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com