Question

10．曲线 y=$\sqrt{x}$与 $y={x^{\frac{3}{2}}}$所围成的封闭图形的面积为（　　）

• A． ．$\frac{1}{2}$
• B． $\frac{4}{15}$
• C． $\frac{2}{3}$
• D． $\sqrt{2}$

Answer 1

分析 先根据题意画出区域，然后依据图形得到积分下限为0，积分上限为1，从而利用定积分表示出曲边梯形的面积，最后用定积分的定义求出所求即可．

解答 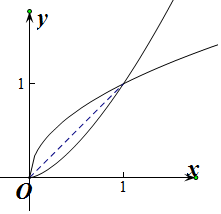解：联立方程组$\left\{\begin{array}{l}{y=\sqrt{x}}\\{y={x}^{\frac{3}{2}}}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$，
则曲线 y=$\sqrt{x}$与 $y={x^{\frac{3}{2}}}$所围成的封闭图形的面积为S=${∫}_{0}^{1}$（$\sqrt{x}$-x）dx+${∫}_{0}^{1}$（x-${x}^{\frac{3}{2}}$）dx=（$\frac{2}{3}{x}^{\frac{3}{2}}$-$\frac{1}{2}{x}^{2}$）|${\;}_{0}^{1}$+（$\frac{1}{2}{x}^{2}$-$\frac{2}{5}{x}^{\frac{5}{2}}$）|${\;}_{0}^{1}$=（$\frac{2}{3}$-$\frac{1}{2}$）+（$\frac{1}{2}$-$\frac{2}{5}$）=$\frac{4}{15}$，
故选：B

点评 本题主要考查了学生会求出原函数的能力，以及考查了数形结合的思想，同时会利用定积分求图形面积的能力，解题的关键就是求原函数．