
| A. | 1 | B. | -1 | C. | $\frac{24}{25}$ | D. | -$\frac{4}{5}$ |
分析 由已知求出cos(α-β),sin(α+β)的值,再由cos2β=cos[(α+β)-(α-β)],展开两角差的余弦求解.
解答 解:由sin(α-β)=$\frac{3}{5}$,cos(α+β)=-$\frac{3}{5}$,且α-β∈($\frac{π}{2}$,π),α+β∈($\frac{π}{2}$,π),
得cos(α-β)=$-\sqrt{1-si{n}^{2}(α-β)}=-\sqrt{1-(\frac{3}{5})^{2}}=-\frac{4}{5}$,sin(α+β)=$\sqrt{1-co{s}^{2}(α+β)}=\sqrt{1-(-\frac{3}{5})^{2}}=\frac{4}{5}$,
∴cos2β=cos[(α+β)-(α-β)]=cos(α+β)cos(α-β)+sin(α+β)sin(α-β)
=(-$\frac{4}{5}$)×(-$\frac{3}{5}$)+$\frac{4}{5}×\frac{3}{5}$=$\frac{24}{25}$.
故选:C.
点评 本题考查两角和与差的余弦,关键是“拆角配角”思想的运用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -24 | B. | 24 | C. | -24$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{6}=1$ | B. | $\frac{{y}^{2}}{3}-\frac{{x}^{2}}{6}=1$ | C. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{4}=1$ | D. | $\frac{{y}^{2}}{4}-\frac{{x}^{2}}{8}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
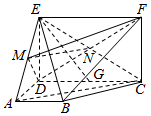 如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.
如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com