
分析 通过对数运算法则化简已知条件,利用换元法结合线性规划求解所求表达式的范围即可.
解答 解:正实数x,y,z满足0≤log2x-log${\;}_{\sqrt{2}}$y+log2z≤1,且x+y≤2z,
可得:1≤$\frac{xz}{{y}^{2}}$≤2,$\frac{x}{z}+\frac{y}{z}≤2$,x,y,z>0.
令$\frac{x}{z}=a$,$\frac{y}{z}=b$,
不等式转化为:1≤$\frac{a}{{b}^{2}}$≤2,0<a+b≤2,
则$\frac{x-y}{z}$=a-b.
画出$\frac{1}{2}a≤{b}^{2}≤a$,0<a+b≤2表示的可行域如图: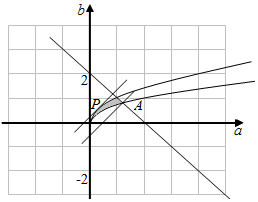
当t=a-b与b2=a相切时$\frac{x-y}{z}$取得最小值:
$\left\{\begin{array}{l}{{b}^{2}=a}\\{t=a-b}\end{array}\right.$,可得b2-b-t=0,△=1+4t=0,解得t=-$\frac{1}{4}$.即:$\frac{x-y}{z}$≥$-\frac{1}{4}$
当t=a-b结果可行域的A时,取得最大值:此时$\left\{\begin{array}{l}{2{b}^{2}=a}\\{a+b=2}\end{array}\right.$,解得A($\frac{9-\sqrt{17}}{4}$,$\frac{-1+\sqrt{17}}{4}$),
可得$\frac{x-y}{z}$≤$\frac{5-\sqrt{17}}{2}$.
$\frac{x-y}{z}$的取值范围为:[-$\frac{1}{4}$,$\frac{5-\sqrt{17}}{2}$].
故答案为:[-$\frac{1}{4}$,$\frac{5-\sqrt{17}}{2}$].
点评 本题考查线性规划的简单应用,换元法的应用,考查数形结合转化思想的应用.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{m}^{2}}$ | B. | $\frac{1}{m}$ | C. | 2m | D. | $\frac{2}{m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\frac{1}{e}$) | C. | [e,+∞) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则|$\overrightarrow{a}$|-|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$| | B. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| | ||
| C. | 若|$\overrightarrow{a}$|-|$\overrightarrow{b}$|<|$\overrightarrow{a}$+$\overrightarrow{b}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$不共线 | D. | 若$\overrightarrow{a}$,$\overrightarrow{b}$不共线,则|$\overrightarrow{a}$+$\overrightarrow{b}$|<|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{24}{25}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
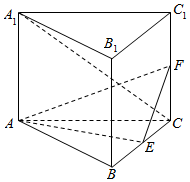 如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.
如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com