
分析 (Ⅰ)求出f(x)的导数,讨论当a≥0时,a<-$\frac{e}{2}$时,a=-$\frac{e}{2}$时,-$\frac{e}{2}$<a<0,由导数大于0,可得增区间;由导数小于0,可得减区间;
(Ⅱ)由(Ⅰ)的单调区间,对a讨论,结合单调性和函数值的变化特点,即可得到所求范围.
解答 解:(Ⅰ)由f(x)=(x-2)ex+a(x-1)2,
可得f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a),
①当a≥0时,由f′(x)>0,可得x>1;由f′(x)<0,可得x<1,
即有f(x)在(-∞,1)递减;在(1,+∞)递增;
②当a<0时,若a=-$\frac{e}{2}$,则f′(x)≥0恒成立,即有f(x)在R上递增;
若a<-$\frac{e}{2}$时,由f′(x)>0,可得x<1或x>ln(-2a);
由f′(x)<0,可得1<x<ln(-2a).
即有f(x)在(-∞,1),(ln(-2a),+∞)递增;
在(1,ln(-2a))递减;
若-$\frac{e}{2}$<a<0,由f′(x)>0,可得x<ln(-2a)或x>1;
由f′(x)<0,可得ln(-2a)<x<1.
即有f(x)在(-∞,ln(-2a)),(1,+∞)递增;
在(ln(-2a),1)递减;
(Ⅱ)
①由(Ⅰ)可得当a>0时,f(x)在(-∞,1)递减;在(1,+∞)递增,
且f(1)=-e<0,x→+∞,f(x)→+∞;x→-∞,f(x)→+∞.f(x)有两个零点;
②当a=0时,f(x)=(x-2)ex,所以f(x)只有一个零点x=2;
③当a<0时,
若a<-$\frac{e}{2}$时,f(x)在(1,ln(-2a))递减,在(-∞,1),(ln(-2a),+∞)递增,
又当x≤1时,f(x)<0,所以f(x)不存在两个零点;
当a≥-$\frac{e}{2}$时,f(x)在(1,+∞)单调递增,又x≤1时,f(x)<0,所以f(x)不存在两个零点.
综上可得,f(x)有两个零点时,a的取值范围为(0,+∞).
点评 本题考查导数的运用:求单调区间,考查函数零点的判断,注意运用分类讨论的思想方法和函数方程的转化思想,考查化简整理的运算能力,属于难题.


 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:选择题
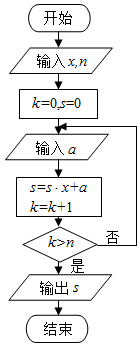 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )| A. | 7 | B. | 12 | C. | 17 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
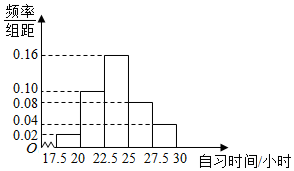 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )| A. | 56 | B. | 60 | C. | 120 | D. | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com