
 如图,有一壁画,最高点A处离地面AO=4m,最低点B处离地面BO=2m,观赏它的C点在过墙角O点与地面成30°角的射线上.
如图,有一壁画,最高点A处离地面AO=4m,最低点B处离地面BO=2m,观赏它的C点在过墙角O点与地面成30°角的射线上.分析 (1)过C作CD⊥AO,垂足为D,则θ=∠ACD-∠BCD,利用差角的正切公式,求tanθ的值;
(2)利用差角的正切公式,我们可以求得tanθ,利用基本不等式可得结论.
解答 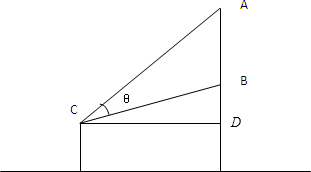 解:(1)作CD⊥AO于D,则$CD=x=\sqrt{3}$,
解:(1)作CD⊥AO于D,则$CD=x=\sqrt{3}$,
在直角△CDO中,$DO=\frac{{\sqrt{3}}}{3}x=1$,…(2分)
$tan∠BCD=\frac{BO-OD}{CD}=\frac{1}{{\sqrt{3}}}$,$tan∠ACD=\frac{AO-OD}{CD}=\sqrt{3}$,
因∠BCD,∠ACD都为锐角,所以∠BCD=30°,∠ACD=60°,…(4分)
所以$tanθ=tan{30^0}=\frac{{\sqrt{3}}}{3}$;…(6分)
(2)设∠BCD=α,∠ACD=β.作如下规定:
当D点在B点下方时α为正,当D点在B点上方时α为负,当D点与B重合时α为零.类似地β也如此规定.
于是有$α,β∈(-\frac{π}{2},\frac{π}{2})$,θ=β-α,…(8分)
$tanα=\frac{BO-OD}{CD}=\frac{{2-\frac{{\sqrt{3}}}{3}x}}{x}$,$tanβ=\frac{AO-OD}{CD}=\frac{{4-\frac{{\sqrt{3}}}{3}x}}{x}$…(10分)
$tanθ=tan(β-α)=\frac{tanβ-tanα}{1+tanβ•tanα}$=$\frac{{\frac{{4-\frac{{\sqrt{3}}}{3}x}}{x}-\frac{{2-\frac{{\sqrt{3}}}{3}x}}{x}}}{{1+\frac{{4-\frac{{\sqrt{3}}}{3}x}}{x}•\frac{{2-\frac{{\sqrt{3}}}{3}x}}{x}}}$=$\frac{2}{{\frac{4}{3}x+\frac{8}{x}-2\sqrt{3}}}$…(12分)$≤\frac{2}{{2\sqrt{\frac{4}{3}x•\frac{8}{x}}-2\sqrt{3}}}=\frac{{\sqrt{3}}}{{4\sqrt{2}-3}}$…(14分)
当且仅当$\frac{4}{3}x=\frac{8}{x}$,$x=\sqrt{6}$时tanθ最大,从而θ最大,此时C点离墙$\sqrt{6}m$.…(16分)
点评 本题以实际问题为载体,考查差角的正切函数公式,考查基本不等式的运用,解题的关键是利用差角的正切函数公式构建函数模型.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | -45 | C. | 1335 | D. | -1335 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-5≤x<-1} | B. | {x|-5≤x<5} | C. | {x|-1<x≤1} | D. | {x|1≤x<5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com