练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】高一数学竞赛共设有35个考场，甲、乙、丙三所学校的领队各自将本校学生人数相同的考场归为一组.经统计，甲校共有i组，各组的考场数分别为；乙校共有j组，各组的考场数分别为；丙校共有k组，各组的考场数分别为.已知包含了1 ~ 14的所有整数.证明：能找到三个考场，至少有两所学校在这三个考场中的选手人数各自是相同的.

    【答案】见解析

    【解析】

    令.

    因为包含了1 ~ 14的整数，所以.

    而

    .

    于是，恰是1，2，…，14的一个排列.

    因此，.

    接下来证明：能找到三个考场，使得它们中至少有两所学校，每所学校选手的人数分别相同.

    不妨设，这14个考场记为A组，是甲校选手人数相同的14个考场，由于每个考场中还有乙校和丙校的选手，它还可归入其他两所学校的分组.由，知必有乙校分出的组数j或丙校分出的组数k不大于6，不妨设乙校分出的组数j不大于6.

    A组的14个考场分到这不超过6个乙校分出的组中去，必有一组是至少三个A组的考场，显然，这三个A组考场的甲校选手人数相同，而这三个考场又是同属于乙校分组中的某一组，它们乙校选手人数也相同.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知△DEF三边所在的直线分别为l1:x=－2，l2：x+y－4=0，l3：x－y－4=0，⊙C为△DEF的内切圆.

    （1）求⊙C的方程；

    （2）设⊙C与x轴交于A、B两点，点P在⊙C内，且满足.记直线PA、PB的斜率分别为k1、k2，求k1 k2的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，．

    （1）求证：；

    （2）试在线段上找一点，使平面，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设有关于x的一元二次方程x2+2ax+b2=0.

    (1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.

    (2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=
    （1）求函数f（x）的定义域A；
    （2）设B={x|﹣1＜x＜2}，当实数a、b∈（B∩RA）时，证明： |．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体ABCDE中，DB⊥平面ABC，AE∥DB，且△ABC为等边三角形，AE=1，BD=2，CD与平面ABCDE所成角的正弦值为 ．

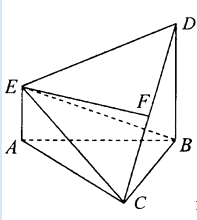
    （1）若F是线段CD的中点，证明：EF⊥平面DBC；
    （2）求二面角D﹣EC﹣B的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=2x，g（x）是一次函数，并且点（2，2）在函数f[（g（x）]的图象上，点（2，5）在函数g[f（x）]的图象上，则g（x）的解析式为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方形ABCD中，AB=AD=2，M，N分别是边BC，CD上的动点，且MN= ，则 的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C的对边分别是a，b，c，已知c=6，sinA﹣sinC=sin（A﹣B）．若1≤a≤6，则sinC的取值范围是 ．

    查看答案和解析>>

    同步练习册答案