
分析 (1)求得已知圆的圆心和半径,设k=$\frac{y}{x}$,即kx-y=0,则圆心到直线的距离d≤r,加上即可得到最值;
(2)x2+y2+2x+3=(x+1)2+y2+2表示点(x,y)与A(-1,0)的距离的平方加上2,连接AC,交圆C于B,延长AC,交圆于D,可得AB最短,AD最长,加上即可得到所求最值;
(3)化简可得(x-3)2+(y-3)2=4,从而令x-3=2cosa,y-3=2sina,从而利用三角函数求最值.
解答 解:如图示: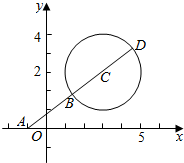 ,
,
(1)圆x2+y2-6x-6y+14=0即为(x-3)2+(y-3)2=4,
可得圆心为C(3,3),半径为r=2,
设k=$\frac{y}{x}$,即kx-y=0,
则圆心到直线的距离d≤r,
即 $\frac{|3k-3|}{\sqrt{1{+k}^{2}}}$≤2,
平方得5k2-18k+5≤0,
解得:$\frac{9-2\sqrt{14}}{5}$≤k≤$\frac{9+2\sqrt{14}}{5}$,
故$\frac{y}{x}$的最大值是$\frac{9+2\sqrt{14}}{5}$,最小值为$\frac{9-2\sqrt{14}}{5}$;
(2)x2+y2+2x+3=(x+1)2+y2+2
表示点(x,y)与A(-1,0)的距离的平方加上2,
连接AC,交圆C于B,延长AC,交圆于D,
可得AB为最短,且为|AC|-r=$\sqrt{16+9}$-2=3,
AD为最长,且为|AC|+r=5+2=7,
则x2+y2+2x+3 的最大值为72+2=51,
x2+y2+2x+3的最小值为32+2=11;
(3)圆x2+y2-6x-6y+14=0即为(x-3)2+(y-3)2=4,
令x-3=2cosa,y-3=2sina,
则x+y=6+2(cosa+sina)=6+2$\sqrt{2}$sin(a+$\frac{π}{4}$),
∵-1≤sin(a+$\frac{π}{4}$)≤1,
∴6-2$\sqrt{2}$≤6+2$\sqrt{2}$sin(a+$\frac{π}{4}$)≤6+2$\sqrt{2}$,
∴x+y的最大值为6+2$\sqrt{2}$,最小值为6-2$\sqrt{2}$.
点评 本题主要考查直线和圆的方程的应用,根据圆心到直线的距离和半径之间的关系以及连接圆外一点与圆心的直线与圆的交点,取得最值是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 23 | C. | 34 | D. | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
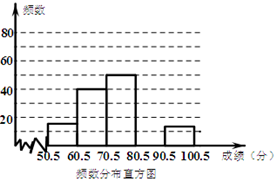 2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:| 分数段 | 频数 | 频率 |
| 50.5~60.5 | 16 | 0.08 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 50 | 0.25 |
| 80.5~90.5 | m | 0.35 |
| 90.5~100.5 | 24 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com