
分析 (1)先求导,再根据导数和函数的单调性和最值的关系,分类讨论,即可求出a的值.
(2)先求f(x)的导函数,得到f′(x0),在利用斜率公式求出过这两点的斜率公式,利用构造函数并利用构造函数的单调性比较大小;
解答 解:(1)f(x)=lnx,$g(x)=\frac{a}{x}(a>0)$,
∴F(x)=f(x)+g(x)=lnx+$\frac{a}{x}$,x>0,
∴F′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,x>0,
当F′(x)>0时,解得x>a,函数单调递增,
当F′(x)<0时,解得0<x<a,函数单调递减,
∵x∈[1,e],
当0<a≤1时,F′(x)在[1,e]上单调递增,F(x)min=F(1)=a=$\frac{3}{2}$,不合题意,
当1<a<e时,F′(x)在[1,a]上单调递减,在(a,e]上函数单调递增,
∴F(x)min=F(a)=lna+1=$\frac{3}{2}$,解得a=$\sqrt{e}$,
当a≥e,F′(x)在[1,e]上单调递减,F(x)min=F(e)=1+$\frac{a}{e}$=$\frac{3}{2}$,解得a=$\frac{e}{2}$,不合题意,
综上所述a=$\sqrt{e}$,
(2)∵A(x1,y1),B(x2,y2)是函数f(x)图象上任意不同的两点,
设线段AB的中点(x0,y0),
当a=1时,g(x)=$\frac{1}{x}$,
∴g($\frac{{x}_{1}+{x}_{2}}{2}$)=g(x0)
∵f(x)=lnx,
∴f′(x)=$\frac{1}{x}$,
∴g(x0)=f′(x0),
∵设A(x1,y1),B(x2,y2)是函数f(x)图象上任意不同的两点,
∴k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{2-}{x}_{1}}$=$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$
不妨设x2>x1,只要比较k与f'(x0)的大小,
即比较$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$与$\frac{2}{{x}_{1}+{x}_{2}}$的大小
又∵x2>x1,
∴即比较ln$\frac{{x}_{2}}{{x}_{1}}$与$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$=$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{\frac{{x}_{2}}{{x}_{1}}+1}$的大小.
令h(x)=lnx-$\frac{2(x-1)}{x+1}$,(x≥1),
则h′(x)=$\frac{1}{x}$-$\frac{4}{(x+1)^{2}}$=$\frac{(x-1)^{2}}{x(x+1)^{2}}$≥0
∴h(x)在[1,+∞)上是增函数.
又$\frac{{x}_{2}}{{x}_{1}}$>1,
∴h($\frac{{x}_{2}}{{x}_{1}}$)>h(1)=0,
∴ln$\frac{{x}_{2}}{{x}_{1}}$>$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{\frac{{x}_{2}}{{x}_{1}}+1}$,
∴k>f′(x0),
∴$k>g(\frac{{{x_1}+{x_2}}}{2})$.
点评 本题考查了利用导函数求函数的最值,还考查了构造函数并利用构造的函数的单调性把问题转化为恒成立的问题,重点考查了学生的转化的思想及构造的函数与思想.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
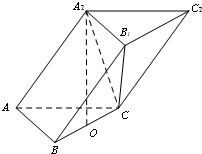 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=$\sqrt{5}$,BC=4,BC的中点为O,A1O垂直于底面ABC.
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=$\sqrt{5}$,BC=4,BC的中点为O,A1O垂直于底面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com