
���� ��1����������ƽ����ͬ�ǵ�ƽ����ϵ�����ɵõ�C1����ͨ���̣�����x=��cos�ȣ�y=��sin�ȣ��Լ����Ǻ͵����ҹ�ʽ������ɵ�C2��ֱ�����귽�̣�
��2��������ɵõ�ֱ��x+y-4=0��ƽ��������Բ����ʱ��|PQ|ȡ����ֵ������ֱ��x+y-4=0ƽ�е�ֱ�߷���Ϊx+y+t=0��������Բ���̣������б�ʽΪ0�����t������ƽ���ߵľ��빫ʽ���ɵ�|PQ|����Сֵ���ⷽ�̿ɵ�P��ֱ�����꣮
���⣺��P��$\sqrt{3}$cos����sin�������ɵ㵽ֱ�ߵľ��빫ʽ����ϸ����ǹ�ʽ�����Һ�����ֵ���ɵõ�������Сֵ��P�����꣮
��� �⣺��1������C1�IJ�������Ϊ$\left\{\begin{array}{l}{x=\sqrt{3}cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������
���������ƽ���ɵ�$\frac{{x}^{2}}{3}$+y2=cos2��+sin2��=1��
������ԲC1��$\frac{{x}^{2}}{3}$+y2=1��
����C2�ļ����귽��Ϊ��sin����+$\frac{��}{4}$��=2$\sqrt{2}$��
���Цѣ�$\frac{\sqrt{2}}{2}$sin��+$\frac{\sqrt{2}}{2}$cos�ȣ�=2$\sqrt{2}$��
��x=��cos�ȣ�y=��sin�ȣ��ɵ�x+y-4=0��
����C2��ֱ�����귽��Ϊֱ��x+y-4=0��
��2��������ɵõ�ֱ��x+y-4=0��ƽ��������Բ����ʱ��
|PQ|ȡ����ֵ��
����ֱ��x+y-4=0ƽ�е�ֱ�߷���Ϊx+y+t=0��
����$\left\{\begin{array}{l}{x+y+t=0}\\{{x}^{2}+3{y}^{2}=3}\end{array}\right.$�ɵ�4x2+6tx+3t2-3=0��
��ֱ������Բ���У��ɵá�=36t2-16��3t2-3��=0��
���t=��2��
��Ȼt=-2ʱ��|PQ|ȡ����Сֵ��
����|PQ|=$\frac{|-4-��-2��|}{\sqrt{1+1}}$=$\sqrt{2}$��
��ʱ4x2-12x+9=0�����x=$\frac{3}{2}$��
��ΪP��$\frac{3}{2}$��$\frac{1}{2}$����
���⣺��P��$\sqrt{3}$cos����sin������
��P��ֱ�ߵľ���Ϊd=$\frac{|\sqrt{3}cos��+sin��-4|}{\sqrt{2}}$
=$\frac{|2sin����+\frac{��}{3}��-4|}{\sqrt{2}}$��
��sin����+$\frac{��}{3}$��=1ʱ��|PQ|����СֵΪ$\sqrt{2}$��
��ʱ��ȡ��=$\frac{��}{6}$������P��$\frac{3}{2}$��$\frac{1}{2}$����
���� ���⿼��������̺���ͨ���̵Ļ������������ֱ������Ļ�����ͬʱ����ֱ������Բ��λ�ù�ϵ����Ҫ�����У����黯�����������������������е��⣮


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
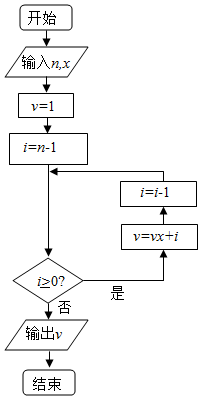 �ؾ������ҹ�����ʱ�ڵ���ѧ�ң����ݣ����Ĵ�ʡ�����أ��ˣ����������ġ�������¡�������Ķ���ʽ��ֵ���ؾ����㷨���������DZȽ��Ƚ����㷨����ͼ��ʾ�ij����ͼ�����������ؾ����㷨��ij����ʽֵ��һ��ʵ����������n��x��ֵ�ֱ�Ϊ3��2�������v��ֵΪ��������
�ؾ������ҹ�����ʱ�ڵ���ѧ�ң����ݣ����Ĵ�ʡ�����أ��ˣ����������ġ�������¡�������Ķ���ʽ��ֵ���ؾ����㷨���������DZȽ��Ƚ����㷨����ͼ��ʾ�ij����ͼ�����������ؾ����㷨��ij����ʽֵ��һ��ʵ����������n��x��ֵ�ֱ�Ϊ3��2�������v��ֵΪ��������| A�� | 9 | B�� | 18 | C�� | 20 | D�� | 35 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | i | D�� | -i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com