
分析 (Ⅰ)由x=ρcosθ,y=ρsinθ,利用曲线C的直角坐标方程能求出曲线C的极坐标方程.
(Ⅱ)由$\left\{\begin{array}{l}{ρ=2cosθ}\\{θ=\frac{π}{3}}\end{array}\right.$,得点P的极坐标为P(1,$\frac{π}{3}$),由$\left\{\begin{array}{l}{2ρsin(θ+\frac{π}{3})+3\sqrt{3}=0}\\{θ=\frac{π}{3}}\end{array}\right.$,得Q的极坐标为Q(-3,$\frac{π}{3}$),由此能求出线段PQ的长.
解答 解:(Ⅰ)因为x=ρcosθ,y=ρsinθ,
曲线C的方程为:(x-1)2+y2=1,即x2+y2-2x=0,
所以曲线C的极坐标方程为ρ2-2ρcosθ=0,即ρ=2cosθ. …(4分)
(Ⅱ)∵直线l1的极坐标方程是2ρsin(θ+$\frac{π}{3}$)+3$\sqrt{3}$=0,
直线l2:θ=$\frac{π}{3}$(ρ∈R)与曲线C交于O、P两点,
设P(ρ1,θ1),则由$\left\{\begin{array}{l}{ρ=2cosθ}\\{θ=\frac{π}{3}}\end{array}\right.$,解得${ρ}_{1}=1,{θ}_{1}=\frac{π}{3}$.
即点P的极坐标为P(1,$\frac{π}{3}$).…(6分)
设Q(ρ2,θ2),则有$\left\{\begin{array}{l}{2ρsin(θ+\frac{π}{3})+3\sqrt{3}=0}\\{θ=\frac{π}{3}}\end{array}\right.$,解得${ρ}_{2}=-3,{θ}_{2}=\frac{π}{3}$,…(9分)
即点Q的极坐标为Q(-3,$\frac{π}{3}$),
所以线段PQ的长|PQ|=|ρ1-ρ2|=4.…(10分)
点评 本题考查曲线的极坐标方程的求法,考查线段长的求法,涉及到极坐标方程、参数方程、直角坐标方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(2)}{f(0)}>2,\frac{f(0)}{{f({-2})}}>2$ | B. | f(2)>2f(0)>4f(-2) | C. | $\frac{f(2)}{f(0)}<2,\frac{f(0)}{{f({-2})}}<2$ | D. | f(2)<2f(0)<4f(-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
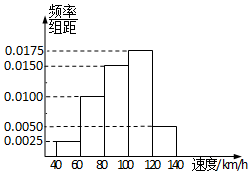 根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.
根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com