考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(I)由已知得
f′(x)=-2ax+(2-a)=-,由此利用导数性质能求出f(x)的单调性.(II)设
g(x)=f(+x)-f(-x),则g(x)=ln(1+ax)-ln(1-ax)-2ax,由此利用导数性质能证明当a>0且0<x<
时,f(
+x)>f(
-x).
解答:
(I)解:f(x)的定义域为(0,+∞),
f′(x)=-2ax+(2-a)=-,
①若a≤0,f'(x)>0,所以f(x)在(0,+∞)单调增加;
②若a>0,则由f'(x)=0得
x=,
且当
x∈(0,)时,f'(x)>0,
当
x>时,f'(x)<0,
所以f(x)在
(0,)单调增加,在
(,+∞)单调减少.
(II)证明:设
g(x)=f(+x)-f(-x),
则g(x)=ln(1+ax)-ln(1-ax)-2ax,
⇒0<x<g′(x)=+-2a=,
当
0<x<时,g'(x)>0,g(x)单增,
而g(0)=0,所以g(x)>0.
故当
0<x<时,
f(+x)>f(-x).
点评:本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力.解题时要认真审题,注意导数性质的合理运用.



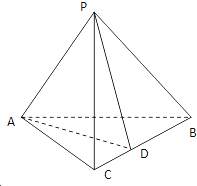 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,点D为BC中点.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,点D为BC中点.