
(本小题9分)如图所示, ⊥平面
⊥平面 ,
,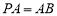 ,
,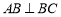 ,
,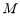 为
为 中点.
中点.
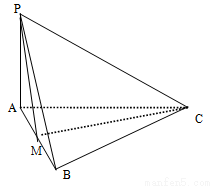
(1)证明: ;
;
(2)若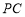 与平面
与平面 所成角的正切值 为
所成角的正切值 为 ,求二面角
,求二面角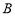 -
- -
- 的正弦值.
的正弦值.
(1)证明见解析,(2)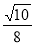
【解析】
试题分析:欲证 ,只需证明
,只需证明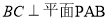 ,
,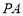 ⊥平面
⊥平面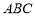 ,有
,有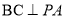 ,又由已知
,又由已知
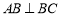 ,所以
,所以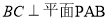 即可;第二步求二面角,先建立空间直角坐标系,过
即可;第二步求二面角,先建立空间直角坐标系,过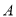 作
作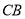 的平行线
的平行线
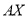 ,以
,以 为原点,分别以
为原点,分别以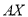 ,
,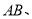
 为
为 轴,建立空间直角坐标系
轴,建立空间直角坐标系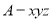 ,写出相应点的
,写出相应点的
坐标,分别求平面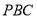 和平面
和平面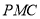 的法向量的法向量,最后求出二面角的余弦值,在化为正弦值即可.
的法向量的法向量,最后求出二面角的余弦值,在化为正弦值即可.
试题解析:(1)因为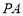 ⊥平面
⊥平面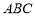 ,
, ,有
,有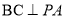 ,又由已知
,又由已知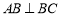 ,
,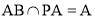
所以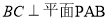 ,又
,又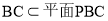 ,则
,则 ;
;
(2)因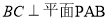 ,
,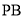 为
为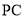 在平面
在平面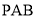 内的射影,
内的射影, 为
为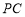 与平面
与平面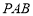 所成角,不妨设
所成角,不妨设
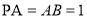 ,
,
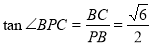 ,则
,则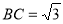 ,
,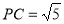 ,过
,过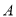 作
作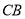 的平行线
的平行线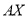 ,
,
以 为原点,分别以
为原点,分别以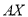 ,
,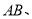
 为
为 轴,建立空间直角坐标系
轴,建立空间直角坐标系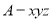 ,则A(0,0,0),
,则A(0,0,0),
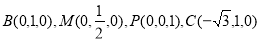 ,设平面
,设平面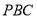 的法向量为
的法向量为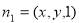 ,因
,因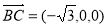 ,
,
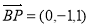 ,
, ,
,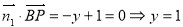 ,
,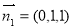 ,设
,设
平面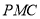 的法向量
的法向量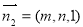 ,
,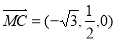 ,
, ,
, ,
,
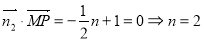 ,
,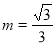 ,
,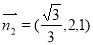 ,设二面角为
,设二面角为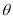 ,因为二面角是锐角,则
,因为二面角是锐角,则
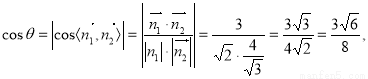 ,
,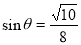 .
.
考点:1.面面垂直的判定和性质;2.利用法向量求二面角;3.直线和平面所成的角


科目:高中数学 来源:2014-2015学年湖北省武汉市武昌区高三元月调研考试理科数学试卷(解析版) 题型:选择题
如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面 上.用一平行于平面
上.用一平行于平面 的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为
的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为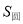 和
和 ,那么
,那么

A.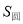
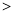
 B.
B.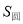 =
= C.
C.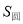
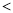
 D.不确定
D.不确定
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三上学期期末质量检测理科数学试卷(解析版) 题型:选择题
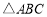 的三个内角
的三个内角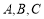 所对的边分别为
所对的边分别为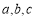 . 若
. 若 ,则角
,则角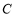 的大小为( ).
的大小为( ).
A.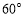 B.
B.  C.
C. D.
D.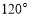
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期第二次统练文科数学试卷(解析版) 题型:填空题
如图,过抛物线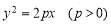 的焦点F的直线
的焦点F的直线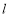 交抛物线于点A、B,交其准线于点C,若
交抛物线于点A、B,交其准线于点C,若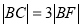 ,且
,且 ,则此抛物线的方程为_____________
,则此抛物线的方程为_____________

查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期第二次统练文科数学试卷(解析版) 题型:选择题
如图所示,正方体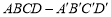 的棱长为1,
的棱长为1, 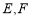 分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱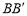 、
、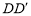 交于
交于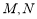 ,设
,设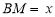 ,
, ,给出以下四个命题:
,给出以下四个命题:

(1)平面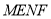
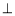 平面
平面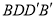 ;
;
(2)当且仅当x=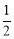 时,四边形
时,四边形 的面积最小;
的面积最小;
(3)四边形 周长
周长 ,
, 是单调函数;
是单调函数;
(4)四棱锥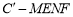 的体积
的体积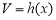 为常函数;
为常函数;
以上命题中假命题的序号为( )
A.(1)(4) B.(2) C.(3) D.(3)(4)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期第二次统练理科数学试卷(解析版) 题型:填空题
若不全为零的实数 成等差数列,点
成等差数列,点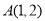 在动直线
在动直线 上的射影为
上的射影为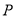 ,点Q在直线
,点Q在直线 上,则线段PQ长度的最小值是__________
上,则线段PQ长度的最小值是__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com