
| A. | ②③ | B. | ②④ | C. | ①②④ | D. | ①②③④ |
分析 命题p:利用指数函数的单调性可得:xa>xb,是真命题;命题q:若x2-ax+1>0恒成立,则△<0,解出即可判定真假;再利用复合命题真假的判定方法.
解答 解:命题p:∵0<a<1,b>1,x∈(0,1),则xa>xb,是真命题;
命题q:若x2-ax+1>0恒成立,则△=a2-4<0,解得-2<a<2,而非-2≤a≤2,因此是假命题;
可得:①命题“p∧q”是假命题,因此不正确; ②命题“p∧(¬q)”是真命题,正确;
③命题“(¬p)∨q”是假命题,因此不正确; ④命题“(¬p)∨(¬q)”是真命题,正确.
故正确的是②④.
故选:B.
点评 本题考查了指数函数的单调性、复合命题真假的判定方法、一元二次方程的实数根与判别式的关系,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
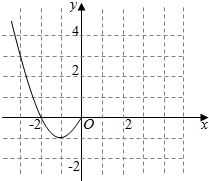 已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象:
已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<n<m | B. | n<m<0 | C. | 0<m<n | D. | m<n<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com