
分析 画出图形,结合图形,先求出$\overrightarrow{AB}$•$\overrightarrow{DC}$的值,再利用$\overrightarrow{AD}$•$\overrightarrow{BC}$=15,即可求出$\overrightarrow{AC}$•$\overrightarrow{BD}$的值.
解答 解:如图所示,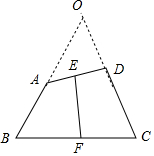
设AB∩DC=O,∵$\overrightarrow{AB}$=$\overrightarrow{AE}$+$\overrightarrow{EF}$+$\overrightarrow{EB}$=$\overrightarrow{EF}$+$\frac{\overrightarrow{AD}-\overrightarrow{BC}}{2}$,$\overrightarrow{DC}$=$\overrightarrow{DE}$+$\overrightarrow{EF}$+$\overrightarrow{FC}$=$\overrightarrow{EF}$+$\frac{\overrightarrow{BC}-\overrightarrow{AD}}{2}$,
两式相加得$\overrightarrow{EF}$=$\frac{\overrightarrow{AB}+\overrightarrow{DC}}{2}$;
∵AB=$\sqrt{2}$,EF=1,CD=$\sqrt{3}$,
平方得1=$\frac{2+3+2\overrightarrow{AB}•\overrightarrow{DC}}{4}$;
∴$\overrightarrow{AB}$•$\overrightarrow{DC}$=-$\frac{1}{2}$;
又∵$\overrightarrow{AD}$•$\overrightarrow{BC}$=15,
即($\overrightarrow{OD}$-$\overrightarrow{OA}$)•($\overrightarrow{OC}$-$\overrightarrow{OB}$)=15;
∴$\overrightarrow{OD}$•$\overrightarrow{OC}$-$\overrightarrow{OD}$•$\overrightarrow{OB}$-$\overrightarrow{OA}$•$\overrightarrow{OC}$+$\overrightarrow{OA}$•$\overrightarrow{OB}$=15,
∴$\overrightarrow{OC}$•$\overrightarrow{OD}$+$\overrightarrow{OA}$•$\overrightarrow{OB}$=15+$\overrightarrow{OD}$•$\overrightarrow{OB}$+$\overrightarrow{OA}$•$\overrightarrow{OC}$,
∴$\overrightarrow{AC}$•$\overrightarrow{BD}$=($\overrightarrow{OC}$-$\overrightarrow{OA}$)•($\overrightarrow{OD}$-$\overrightarrow{OB}$)=$\overrightarrow{OC}$•$\overrightarrow{OD}$-$\overrightarrow{OC}$•$\overrightarrow{OB}$-$\overrightarrow{OA}$•$\overrightarrow{OD}$+$\overrightarrow{OA}$•$\overrightarrow{OB}$
=(15+$\overrightarrow{OD}$•$\overrightarrow{OB}$+$\overrightarrow{OA}$•$\overrightarrow{OC}$)-$\overrightarrow{OC}$•$\overrightarrow{OB}$-$\overrightarrow{OA}$•$\overrightarrow{OD}$
=15+$\overrightarrow{OD}$•($\overrightarrow{OB}$-$\overrightarrow{OA}$)+$\overrightarrow{OC}$•($\overrightarrow{OA}$-$\overrightarrow{OB}$)
=15+$\overrightarrow{OD}$•$\overrightarrow{AB}$+$\overrightarrow{OC}$•$\overrightarrow{BA}$
=15+$\overrightarrow{AB}$•($\overrightarrow{OD}$-$\overrightarrow{OC}$)
=15+$\overrightarrow{AB}$•$\overrightarrow{CD}$
=15-$\overrightarrow{AB}$•$\overrightarrow{DC}$
=15-(-$\frac{1}{2}$)
=$\frac{31}{2}$.
故答案为:$\frac{31}{2}$.
点评 本题考查了两个向量的加减运算的应用问题,也考查了平面向量的几何意义以及平面向量的数量积的应用问题,是综合性题目.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一、二象限 | B. | 第二、三象限 | C. | 第三、四象限 | D. | 第一、四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2-\sqrt{2}$ | B. | $2+\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是正三角形,B1C1∥BC,B1C1=$\frac{1}{2}$BC.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是正三角形,B1C1∥BC,B1C1=$\frac{1}{2}$BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com