练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．设等差数列{an}和等比数列{bn}首项都是1，公差和公比都是2，则a${\;}_{{b}_{2}}$+a${\;}_{{b}_{3}}$+a${\;}_{{b}_{4}}$=（　　）
    A．24B．25C．26D．27

    分析 利用等比数列求出b2，b3，b4，然后利用等差数列求解即可．

    解答 解：等比数列{bn}首项是1，公比是2，
    ∴b2=2，b3=4，
    b4=8，
    等差数列{an}首项是1，公差是2，
    ∴a${\;}_{{b}_{2}}$+a${\;}_{{b}_{3}}$+a${\;}_{{b}_{4}}$=a2+a4+a8=3a1+11d=3+11×2=25．
    故选：B．

    点评 本题考查等差数列以及等比数列的通项公式的应用，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．实数x，y满足$\left\{\begin{array}{l}{2x-y≥0}\\{y≥x}\\{y≥-x+b}\end{array}\right.$，则z=2x+y的最小值为3，则实数b的值为（　　）
    A．$\frac{4}{9}$B．-$\frac{4}{9}$C．$\frac{9}{4}$D．-$\frac{9}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

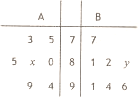    13．某学校从A、B两个班级中各选出7名学生参加市级比赛，他们去得的成绩（满分100分）的茎叶如图所示，其中A班学生成绩的众数是85，B班学生成绩的中位数是83．则x+y的值为8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．命题p：关于x的方程x|x|-2x+m=0（m∈R）有三个实数根；命题q：0≤m＜1；则命题p成立是命题q成立的（　　）
    A．充分而不必要的条件B．必要而不充分的条件
    C．充要条件D．既不充分又不必要的条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

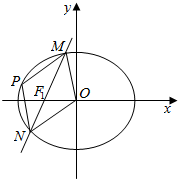    17．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的右顶点、上顶点分别为A、B，坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$，且$a=\sqrt{2}b$．
    （1）求椭圆C的方程；
    （2）过椭圆C的左焦点F1的直线l交椭圆于M、N两点，且该椭圆上存在点P，使得四边形MONP（图形上的字母按此顺序排列）恰好为平行四边形，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．在△ABC中，内角A、B、C的对边分别为a、b、c，已知a-b=2，c=4，sinA=2sinB．
    （1）求△ABC的面积；
    （2）求tan（A-B）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

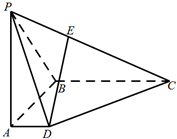    14．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，∠DAB=90°，PA=AB=BC=3，AD=1．
    （Ⅰ）求证：BC⊥平面PAB；
    （Ⅱ）求PC与平面PAB所成角的正切值；
    （Ⅲ）设点E在线段PC上，若$\frac{PE}{EC}$=$\frac{1}{2}$，求证：DE∥平面PAB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．等边三角形ABC的顶点A，B在圆O：x2+y2=1上，则|OC|的最大值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知圆x2+y2+x+2y=$\frac{61}{16}$和圆（x-sinα）2+（y-1）2=$\frac{1}{16}$，其中0°≤α≤90°，则两圆的位置关系是（　　）
    A．相交B．外切C．内切D．相交或内切

    查看答案和解析>>

    同步练习册答案