
【题目】设函数f(x)=x2+ax+b,a,b∈R.
(1)若2a+b=4,证明:|f(x)|在区间[0,4]上的最大值M(a)≥12;
(2)存在实数a,使得当x∈[0,b]时,1≤f(x)≤10恒成立,求实数b的最大值.
【答案】
(1)证明:∵2a+b=4,
∴f(x)=x2+ax+b=x2+ax+4﹣2a= ![]() ,
,
当 ![]() ,即a≥0时,f(x)在[0,4]上为增函数,f(x)∈[﹣2a+4,2a+20],
,即a≥0时,f(x)在[0,4]上为增函数,f(x)∈[﹣2a+4,2a+20],
|f(x)|的最大值为M(a)=2a+20;
当 ![]() ,即a≤﹣8时,f(x)在[0,4]上为减函数,f(x)∈[2a+20,﹣2a+4],
,即a≤﹣8时,f(x)在[0,4]上为减函数,f(x)∈[2a+20,﹣2a+4],
此时﹣2a+4>|2a+20|,|f(x)|的最大值为M(a)=﹣2a+4;
当0 ![]() ,即﹣4≤a<0时,f(x)在[0,4]上的最小值为
,即﹣4≤a<0时,f(x)在[0,4]上的最小值为 ![]() ,
,
f(x)在[0,4]上的最大值为f(4)=2a+20,
∵2a+20≥12,4< ![]() ,
,
∴|f(x)|在区间[0,4]上的最大值M(a)=2a+20;
当 ![]() ,即﹣8<a<﹣4时,f(x)在[0,4]上的最小值为
,即﹣8<a<﹣4时,f(x)在[0,4]上的最小值为 ![]() ,
,
f(x)在[0,4]上的最大值为f(0)=﹣2a+4,
∵﹣2a+4>12,4< ![]() ,
,
∴|f(x)|在区间[0,4]上的最大值M(a)=﹣2a+4.
∴M(a)= ![]() ,则M(a)≥12;
,则M(a)≥12;
(2)解:f(x)=x2+ax+b的对称轴为x= ![]() .
.
①若a≥0,则 ![]() ≤0,∴f(x)在[0,b)上单调递增,
≤0,∴f(x)在[0,b)上单调递增,
∴ ![]() .
.
由b2+ab+b≤10,得 ![]() ≥a≥0,
≥a≥0,
解不等式组 ![]() ,得1
,得1 ![]() .
.
②若0< ![]() <
< ![]() ,即﹣b<a<0时,f(x)在[0,
,即﹣b<a<0时,f(x)在[0, ![]() ]上单调递减,在(﹣
]上单调递减,在(﹣ ![]() ,b]单调递增,
,b]单调递增,
∴  .
.
∴  ,即
,即  ,得1<b<10.
,得1<b<10.
③若0< ![]() <b,即﹣2b<a<﹣b<0时,f(x)在[0,
<b,即﹣2b<a<﹣b<0时,f(x)在[0, ![]() ]单调递减,在(
]单调递减,在( ![]() ,b]单调递增,
,b]单调递增,
∴  ,即
,即 ![]() ,则1<b≤10.
,则1<b≤10.
④若 ![]() ≥b,即a≤﹣2b时,f(x)在[0,b)上单调递减,
≥b,即a≤﹣2b时,f(x)在[0,b)上单调递减,
∴ ![]() ,
,
∴  ,即
,即  ,则b∈.
,则b∈.
综上,b的取值范围是[1,10],b的最大值为10.
【解析】(1)把2a+b=4代入函数解析式,利用f(x)的对称轴为进行分类,求出f(x)在[0,4]上的最值,进一步求得|f(x)|在区间[0,4]上的最大值.由最大值的最小值为12证得答案;(2)f(x)的对称轴为x=﹣ ![]() ,根据对称轴与区间[0,b]的关系分情况讨论f(x)的单调性,求出最值,根据1≤f(x)≤10列出不等式组,化简得出b的取值范围,从而得到实数b的最大值.
,根据对称轴与区间[0,b]的关系分情况讨论f(x)的单调性,求出最值,根据1≤f(x)≤10列出不等式组,化简得出b的取值范围,从而得到实数b的最大值.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,AD=PD=2,PA=2 ![]() ,∠PDC=120°,点E为线段PC的中点,点F在线段AB上.
,∠PDC=120°,点E为线段PC的中点,点F在线段AB上. 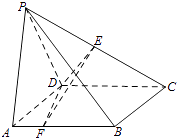
(1)若AF= ![]() ,求证:CD⊥EF;
,求证:CD⊥EF;
(2)设平面DEF与平面DPA所成二面角的平面角为θ,试确定点F的位置,使得cosθ= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自平面上一点O引两条射线OA,OB,P在OA上运动,Q在OB上运动且保持| ![]() |为定值2
|为定值2 ![]() (P,Q不与O重合).已知∠AOB=120°,
(P,Q不与O重合).已知∠AOB=120°,
(I)PQ的中点M的轨迹是的一部分(不需写具体方程);
(II)N是线段PQ上任﹣点,若|OM|=1,则 ![]()
![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系:  (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框![]() ,其中的函数关系式为
,其中的函数关系式为![]() ,程序框图中的
,程序框图中的![]() 为函数
为函数![]() 的定义域.
的定义域.

(1)若输入![]() ,请写出输出的所有
,请写出输出的所有![]() 的值;
的值;
(2)若输出的所有![]() 都相等,试求输入的初始值
都相等,试求输入的初始值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生更多地了解“数学史”知识,某班级举办一次“追寻先哲的足迹,倾听数学的声音的数学史知识竞赛活动.现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:
序号 | 分数段 | 人数 | 频率 |
1 |
| 10 | 0.20 |
2 |
| ① | 0.44 |
3 |
| ② | ③ |
4 |
| 4 | 0.08 |
合计 | 50 | 1 | |
(1)填充上述表中的空格(在解答中直接写出对应空格序号的答案);
(2)若利用组中值近似计算数据的平均数,求此次数学史初赛的平均成绩;
(3)甲同学的初赛成绩在![]() ,学校为了宣传班级的学习经验,随机抽取分数在
,学校为了宣传班级的学习经验,随机抽取分数在![]() 的4位同学中的两位同学到学校其他班级介绍,求甲同学被抽取到的概率.
的4位同学中的两位同学到学校其他班级介绍,求甲同学被抽取到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费每月用电不超过100度仍按原标准收费,超过的部分每度按0.5元计算.
Ⅰ.设月用电x度时,应交电费y元,写出y关于x的函数关系式;
Ⅱ.小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
缴费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com