
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,对
,对![]() ,恒有
,恒有![]() 成立,求实数
成立,求实数![]() 的最小值.
的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图1,直线![]() 将矩形纸
将矩形纸![]() 分为两个直角梯形
分为两个直角梯形![]() 和
和![]() ,将梯形
,将梯形![]() 沿边
沿边![]() 翻折,如图2,在翻折的过程中(平面
翻折,如图2,在翻折的过程中(平面![]() 和平面
和平面![]() 不重合),下面说法正确的是
不重合),下面说法正确的是
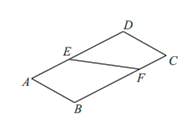
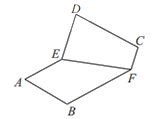
图1 图2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司新发明了甲、乙两种不同型号的手机,公司统计了消费者对这两种型号手机的评分情况,作出如下的雷达图,则下列说法不正确的是( )

A. 甲型号手机在外观方面比较好.B. 甲、乙两型号的系统评分相同.
C. 甲型号手机在性能方面比较好.D. 乙型号手机在拍照方面比较好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“和、平、世、界”四个字,有放回地从中任取一个小球,直到”和””平”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“和、平、世、界”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下24个随机数组:
232 321 230 023 123 021 132 220 011 203 331 100
231 130 133 231 031 320 122 103 233 221 020 132
由此可以估计,恰好第三次就停止的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,等边三角形
中,等边三角形![]() 所在的平面垂直于底面
所在的平面垂直于底面![]() ,
,![]() ,
, ![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判断直线![]() 与平面
与平面![]() 的是否平行,并说明理由.
的是否平行,并说明理由.
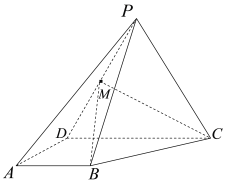
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为![]() ,点A的坐标为
,点A的坐标为![]() ,且
,且![]() .
.
(I)求椭圆的方程;
(II)设直线l: ![]() 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若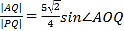 (O为原点) ,求k的值.
(O为原点) ,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com