
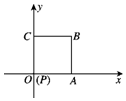
 如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.
如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4. 分析 P点的运动轨迹为若干个$\frac{1}{4}$圆周拼接而成,作出P点轨迹图象,即可得出答案.
解答 解:P点从x轴上开始运动的时候,首先是围绕A点运动$\frac{1}{4}$个圆,该圆半径为2,
然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,
再以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下: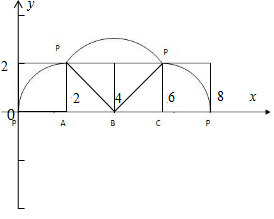
由轨迹可知f(x)的最小正周期为8,
S=2×$\frac{1}{4}$π•22+2×$\frac{1}{2}$×2×2+$\frac{1}{4}$×π•(2$\sqrt{2}$)2=4π+4.
故答案为:8;4π+4.
点评 本题考查的知识点是函数图象的变化,其中根据已知画出正方形转动过程中的一个周期内的图象,利用数形结合的思想对本题进行分析是解答本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $f(x)={({\sqrt{x}})^2}$和$g(x)=\sqrt{x^2}$ | B. | $f(x)={({\root{3}{x+1}})^3}$和$g(x)=\root{3}{{{{({x+1})}^3}}}$ | ||
| C. | f(x)=2lgx和g(x)=lg x2 | D. | f(x)=ln x-ln(x-1)和$g(x)=ln\frac{x}{x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
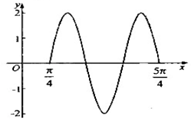 已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).
已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 5 | 4 | 3 | 1 | 2 |
| A. | 2 | B. | 1 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com