
| A. | $f(x)={({\sqrt{x}})^2}$和$g(x)=\sqrt{x^2}$ | B. | $f(x)={({\root{3}{x+1}})^3}$和$g(x)=\root{3}{{{{({x+1})}^3}}}$ | ||
| C. | f(x)=2lgx和g(x)=lg x2 | D. | f(x)=ln x-ln(x-1)和$g(x)=ln\frac{x}{x-1}$ |
分析 分别求出各个选项中函数的定义域,或化简解析式,由函数相等的定义进行判断即可.
解答 解:A、$f(x)={(\sqrt{x})}^{2}$的定义域是(0,+∞),$g(x)=\sqrt{{x}^{2}}$的定义域是R,
即函数f(x)、g(x)不是相等函数,A不正确;
B、$f(x)={(\root{3}{x+1})}^{3}$=x+1,且x∈R,$g(x)=\root{3}{{(x+1)}^{3}}$=x+1,且x∈R,
即函数f(x)、g(x)是相等函数,B正确;
C、f(x)=2lgx的定义域是(0,+∞),g(x)=lg x2的定义域是{x|x≠0},
即函数f(x)、g(x)不是相等函数,C不正确;
D、由$\left\{\begin{array}{l}{x>0}\\{x-1>0}\end{array}\right.$得x>1,函数f(x)的定义域是(0,+∞),
由$\frac{x}{x-1}>0$得x(x-1)>0,解得x>1或x<0,函数g(x)的定义域是(∞,0)∪(1,+∞),
即函数f(x)、g(x)不是相等函数,D不正确,
故选:B.
点评 本题考查函数相等的判断方法:定义法,以及函数定义域的求解,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2016,+∞) | D. | (-∞,0)∪(2016,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
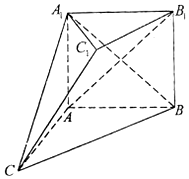 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值16 | B. | 最小值$\frac{1}{16}$ | C. | 最小值16 | D. | 最小值$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
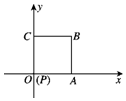 如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.
如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com