
分析 ∨根据f(x)为奇函数,便有f(-x)=-f(x),从而可以求出a=1,从而得到f(x)=1+$\frac{2}{{2}^{x}-1}$,容易判断该函数在(0,+∞)上单调递减,并可判断x<0时,f(x)<1,且f(1)=3,从而可由f(x)>3得到f(x)>f(1),从而便得到0<x<1,这便求出了使f(x)>3成立的x的取值范围.
解答 解:f(x)为奇函数,∴f(-x)=-f(x),⇒$\frac{{{2}^{-}}^{x}+1}{{x}^{-x}-a}=-\frac{{2}^{x}+1}{{2}^{x}-a}$⇒∴1-a•2x=a-2x,∴a=1;
∴f(x)=1+$\frac{2}{{2}^{x}-1}$,
①x>0时,x增大时,2x-1增大,从而f(x)减小;
∴f(x)在(0,+∞)上单调递减;
∴由f(x)>3得,f(x)>f(1);
解得0<x<1;
②x<0时,2x-1<0,∴f(x)<1;
∴不满足f(x)>3;
综上所述,使f(x)>3的x的取值范围为(0,1).
故答案为:(0,1).
点评 考查奇函数的定义,根据单调性定义判断函数单调性的方法,指数函数的单调性,以及根据减函数的定义解不等式的方法.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{7}$ | C. | $\sqrt{13}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
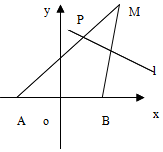 已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.
已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{2}{x}$ | B. | y=x3 | C. | y=-x2 | D. | $y=\sqrt{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)={({\sqrt{x}})^2}$和$g(x)=\sqrt{x^2}$ | B. | $f(x)={({\root{3}{x+1}})^3}$和$g(x)=\root{3}{{{{({x+1})}^3}}}$ | ||
| C. | f(x)=2lgx和g(x)=lg x2 | D. | f(x)=ln x-ln(x-1)和$g(x)=ln\frac{x}{x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
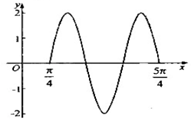 已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).
已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com