
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①,定义域为{x|x≠kπ+$\frac{π}{2}$},关于原点对称,且f(-x)=-f(x),故①为奇函数;
②③,定义域为R关于原点对称,且f(-x)=f(x),故②为偶函数;
④,$y=3sin2({x+\frac{π}{4}})$=3sin(2x+$\frac{π}{2}$)=3cos2x,满足定义域为R关于原点对称\f(-x)=f(x),故④为偶函数,
解答 解:对于①,定义域为{x|x≠kπ+$\frac{π}{2}$},关于原点对称,且f(-x)=-f(x),故①为奇函数,排除①;
对于②③,定义域为R关于原点对称,且f(-x)=f(x),故②为偶函数,故②③满足条件;
对于④,$y=3sin2({x+\frac{π}{4}})$=3sin(2x+$\frac{π}{2}$)=3cos2x,满足定义域为R关于原点对称\f(-x)=f(x),故④为偶函数,满足条件,
故选:D
点评 本题考查奇偶函数的定义,考查学生分析解决问题的能力,比较基础.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
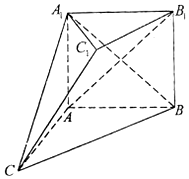 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com