
分析 (Ⅰ) 求导,求得直线PA的方程,将P代入直线方程,求得$x_1^2-2a{x_1}-8=0$,同理可知$x_2^2-2a{x_2}-8=0$.则x1,x2是方程x2-2ax-8=0的两个根,则由韦达定理求得x1x2,y1y2的值,即可求证x1x2+y1y2为定值;设切线方程,代入抛物线方程,由△=0,则k1k2=-2,分别求得切线方程,代入即可求证x1x2+y1y2为定值;
(Ⅱ) 直线PA的垂直平分线方程为$y-\frac{{{y_1}-2}}{2}=-\frac{2}{x_1}({x-\frac{{{x_1}+a}}{2}})$,同理求得直线PB的垂直平分线方程,求得M坐标,抛物线C的焦点为F(0,1),则$\overrightarrow{MF}•\overrightarrow{PF}=\frac{{3{a^2}}}{2}-\frac{{3{a^2}}}{2}=0$,
则$\overrightarrow{MF}⊥\overrightarrow{PF}$.则以PM为直径的圆恒过点F.
解答 解:(Ⅰ)证明:法1:由x2=4y,得$y=\frac{1}{4}{x^2}$,所以$y'=\frac{1}{2}x$.所以直线PA的斜率为$\frac{1}{2}{x_1}$.
因为点A(x1,y1)和B(x2,y2)在抛物线C上,所以${y_1}=\frac{1}{4}x_1^2$,${y_2}=\frac{1}{4}x_2^2$.
所以直线PA的方程为$y-\frac{1}{4}x_1^2=\frac{1}{2}{x_1}({x-{x_1}})$.…(1分)
因为点P(a,-2)在直线PA上,
所以$-2-\frac{1}{4}x_1^2=\frac{1}{2}{x_1}({a-{x_1}})$,即$x_1^2-2a{x_1}-8=0$.…(2分)
同理,$x_2^2-2a{x_2}-8=0$.…(3分)
所以x1,x2是方程x2-2ax-8=0的两个根.
所以x1x2=-8.…(4分)
又${y_1}{y_2}=\frac{1}{4}x_1^2•\frac{1}{4}x_2^2=\frac{1}{16}{({{x_1}{x_2}})^2}=4$,…(5分)
所以x1x2+y1y2=-4为定值.…(6分)
法2:设过点P(a,-2)且与抛物线C相切的切线方程为y+2=k(x-a),…(1分)
$\left\{\begin{array}{l}{y+2=k(x-a)}\\{{x}^{2}=4y}\end{array}\right.$,消去y得x2-4kx+4ka+8=0,
由△=16k2-4(4ak+8)=0,化简得k2-ak-2=0.…(2分)
所以k1k2=-2.…(3分)
由x2=4y,得$y=\frac{1}{4}{x^2}$,所以$y'=\frac{1}{2}x$.
所以直线PA的斜率为${k_1}=\frac{1}{2}{x_1}$,直线PB的斜率为${k_2}=\frac{1}{2}{x_2}$.
所以$\frac{1}{4}{x_1}{x_2}=-2$,即x1x2=-8.…(4分)
又${y_1}{y_2}=\frac{1}{4}x_1^2•\frac{1}{4}x_2^2=\frac{1}{16}{({{x_1}{x_2}})^2}=4$,…(5分)
所以x1x2+y1y2=-4为定值.…(6分)
(Ⅱ) 法1:直线PA的垂直平分线方程为$y-\frac{{{y_1}-2}}{2}=-\frac{2}{x_1}({x-\frac{{{x_1}+a}}{2}})$,…(7分)
由于${y_1}=\frac{1}{4}x_1^2$,$x_1^2-8=2a{x_1}$,
所以直线PA的垂直平分线方程为$y-\frac{{a{x_1}}}{4}=-\frac{2}{x_1}({x-\frac{{{x_1}+a}}{2}})$.①…(8分)
同理直线PB的垂直平分线方程为$y-\frac{{a{x_2}}}{4}=-\frac{2}{x_2}({x-\frac{{{x_2}+a}}{2}})$.②…(9分)
由①②解得$x=\frac{3}{2}a$,$y=1+\frac{a^2}{2}$,
所以点$M({\frac{3}{2}a,1+\frac{a^2}{2}})$.…(10分)
抛物线C的焦点为F(0,1),则$\overrightarrow{MF}=({-\frac{3}{2}a,-\frac{a^2}{2}}),\overrightarrow{PF}=({-a,3})$.
由于$\overrightarrow{MF}•\overrightarrow{PF}=\frac{{3{a^2}}}{2}-\frac{{3{a^2}}}{2}=0$,…(11分)
所以$\overrightarrow{MF}⊥\overrightarrow{PF}$.
所以以PM为直径的圆恒过点F.…(12分)
另法:以PM为直径的圆的方程为$({x-a})({x-\frac{3}{2}a})+({y+2})({y-1-\frac{a^2}{2}})=0$.…(11分)
把点F(0,1)代入上方程,知点F的坐标是方程的解.
所以以PM为直径的圆恒过点F.…(12分)
法2:设点M的坐标为(m,n),
则△PAB的外接圆方程为(x-m)2+(y-n)2=(m-a)2+(n+2)2,
由于点A(x1,y1),B(x2,y2)在该圆上,
则${({{x_1}-m})^2}+{({{y_1}-n})^2}={({m-a})^2}+{({n+2})^2}$,${({{x_2}-m})^2}+{({{y_2}-n})^2}={({m-a})^2}+{({n+2})^2}$.
两式相减得(x1-x2)(x1+x2-2m)+(y1-y2)(y1+y2-2n)=0,①…(7分)
由(Ⅰ)知${x_1}+{x_2}=2a,{x_1}{x_2}=-8,{y_1}=\frac{1}{4}x_1^2,{y_2}=\frac{1}{4}x_2^2$,代入上式得$({{x_1}-{x_2}})({4a-4m+{a^3}+4a-2an})=0$,…(8分)
当x1≠x2时,得8a-4m+a3-2an=0,②
假设以PM为直径的圆恒过点F,则$\overrightarrow{MF}⊥\overrightarrow{PF}$,即(-m,n-1)•(-a,-3)=0,
得ma-3(n-1)=0,③…(9分)
由②③解得$m=\frac{3}{2}a,n=1+\frac{1}{2}{a^2}$,…(10分)
所以点$M({\frac{3}{2}a,1+\frac{1}{2}{a^2}})$.…(11分)
当x1=x2时,则a=0,点M(0,1).
所以以PM为直径的圆恒过点F.…(12分)
点评 本题考查直线与抛物线的位置关系,考查中点坐标公式,韦达定理的应用,考查利用导数求抛物线的切线方程,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | P∧Q | B. | (¬P)∧Q | C. | (¬P)∧(¬Q) | D. | P∧(¬Q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
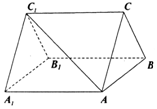 如图所示的三棱柱中,侧面ABB1A1为边长等于2的菱形,且∠AA1B1=60°,△ABC为等边三角形,面ABC⊥面ABB1A1.
如图所示的三棱柱中,侧面ABB1A1为边长等于2的菱形,且∠AA1B1=60°,△ABC为等边三角形,面ABC⊥面ABB1A1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{7}{16}$ | C. | $\frac{1}{2}$ | D. | $\frac{9}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,$\frac{3}{4}$] | C. | [$\frac{1}{3}$,$\frac{2}{3}$] | D. | [$\frac{1}{3}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com