
| A. | (0,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,$\frac{3}{4}$] | C. | [$\frac{1}{3}$,$\frac{2}{3}$] | D. | [$\frac{1}{3}$,$\frac{2}{3}$) |
分析 由减函数可知f(x)在两段上均为减函数,且在第一段的最小值大于或等于第二段上的最大值,作出|f(x)|和y=2-$\frac{x}{3}$的图象,根据交点个数判断3a与2的大小关系,列出不等式组解出.
解答 解: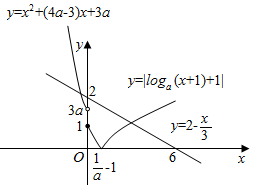 :∵f(x)是R上的单调递减函数,
:∵f(x)是R上的单调递减函数,
∴y=x2+(4a-3)x+3a在(-∞,0)上单调递减,y=loga(x+1)+1在(0,+∞)上单调递减,
且f(x)在(-∞,0)上的最小值大于或等于f(0).
∴$\left\{\begin{array}{l}{\frac{3-4a}{2}≥0}\\{0<a<1}\\{3a≥1}\end{array}\right.$,解得$\frac{1}{3}≤a≤\frac{3}{4}$.
作出y=|f(x)|和y=2-$\frac{x}{3}$的函数草图如图所示:
∵|f(x)|=2-$\frac{x}{3}$恰有两个不相等的实数解,
∴3a<2,即a<$\frac{2}{3}$.
综上,$\frac{1}{3}$≤a<$\frac{2}{3}$.
故选:D.
点评 本题考查了分段函数的单调性,函数零点的个数判断,结合函数函数图象判断端点值的大小是关键,属于中档题.


科目:高中数学 来源: 题型:解答题
| A组 | B组 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2016,+∞) | D. | (-∞,0)∪(2016,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
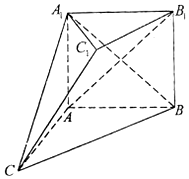 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com