
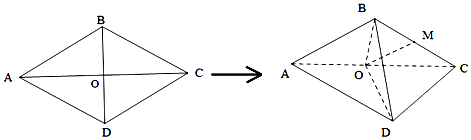
分析 (1)因为点O是菱形ABCD的对角线的交点,所以O是AC的中点.又点M是棱BC的中点,利用三角形中位线定理可得OM∥AB.利用线面平行的判定定理即可证明OM∥平面ABD.
(2)OB=OD=3,BD=3$\sqrt{2}$.利用勾股定理的逆定理可得BO⊥OD,又OD⊥AC,可得OD⊥平面ABC,因此OD=3为三棱锥D-ABC的高,利用三棱锥的体积为V=$\frac{1}{3}{S}_{△ABC}×OD$即可得出.
(3)N是BD上的动点,当点N为BD的中点时,ON⊥BD,此时,ON取得最小值,连接CN,则CN⊥BD.∠CNO为直线CN与平面OBD所成角,此时取得最大角.可得:∠BON为二面角N-AC-B的平面角即可得出.
解答 (1)证明:因为点O是菱形ABCD的对角线的交点,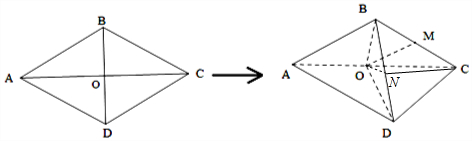
所以O是AC的中点.
又点M是棱BC的中点,
所以OM是△ABC的中位线,OM∥AB.…(2分)
因为OM?平面ABD,
AB?平面ABD,
所以OM∥平面ABD.…(6分)
(2)解:OB=OD=3,BD=3$\sqrt{2}$.
∴OB2+OD2=BD2.
∴∠BOD=90°.
∴BO⊥OD,又OD⊥AC,AC∩OB=O点,
∴OD⊥平面ABC,
所以OD=3为三棱锥D-ABC的高,
因为菱形ABCD的边长为6,∠BAD=60°,
所以S△ABC=$\frac{1}{2}×{6}^{2}×sin12{0}^{°}$=9$\sqrt{3}$,
所以所求三棱锥的体积为V=$\frac{1}{3}{S}_{△ABC}×OD$=$\frac{1}{3}×9\sqrt{3}×3$=9$\sqrt{3}$.
(3)解:N是BD上的动点,当点N为BD的中点时,ON⊥BD,此时,ON取得最小值,
连接CN,则CN⊥BD.∠CNO为直线CN与平面OBD所成角,此时取得最大角.
可得:∠BON为二面角N-AC-B的平面角,可得:∠BON=45°.
∴sin∠BON=$\frac{\sqrt{2}}{2}$.
点评 本题考查了线面平行与垂直的判定定理及其性质定理、三棱锥体积计算公式、空间角,考查了数形结合方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,$\frac{3}{4}$] | C. | [$\frac{1}{3}$,$\frac{2}{3}$] | D. | [$\frac{1}{3}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
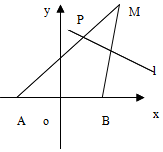 已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.
已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-a2b)2•(-ab2)3=-a7b8 | B. | [-(a3)2•(-b2)3]3=a18b18 | ||
| C. | (-a3)2•(-b2)3=a6b6 | D. | (-a2b3)3÷(-ab2)3=a3b3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{6}}{2}$ | C. | 4 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com