
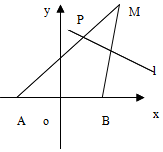
 已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.
已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.分析 (Ⅰ)判断P的轨迹是以A,B为焦点的椭圆,求出a,b,即可求解椭圆的方程.
(Ⅱ)设P(x1,y1),Q(x2,y2)将直线l方程y=kx与椭圆方程联立消y得(1+4k2)x2-16=0,利用弦长公式,表示三角形的面积,利用基本不等式求解最值即可.
解答 解:(Ⅰ)∵|PA|+|PB|=|PA|+|PM|=8;又$|AB|=4\sqrt{3}$,
∴P的轨迹是以A,B为焦点的椭圆,(3分)∵$2a=8,2c=4\sqrt{3}$∴b2=4
因此椭圆的方程为:$\frac{x^2}{16}+\frac{y^2}{4}=1$(4分)
(Ⅱ)设P(x1,y1),Q(x2,y2)
将直线l方程y=kx与椭圆方程联立消y得(1+4k2)x2-16=0,
所以${x^2}=\frac{16}{{1+4{k^2}}}$(6分)
∴$|{PQ}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\sqrt{1+{k^2}}×2×\sqrt{\frac{16}{{1+4{k^2}}}}$(8分)
又∵点A到直线l的距离d=$\frac{{|{2k+1}|}}{{\sqrt{1+{k^2}}}}$(9分)
故△APQ的面积=$\frac{1}{2}|{PQ}|•d=4×\frac{{|{2k+1}|}}{{\sqrt{1+4{k^2}}}}=4×\sqrt{\frac{{4{k^2}+4k+1}}{{1+4{k^2}}}}$
=$4×\sqrt{1+\frac{4k}{{1+4{k^2}}}}=4×\sqrt{1+\frac{4}{{\frac{1}{k}+4k}}}$(11分)
当k>0时,4k+$\frac{1}{k}$≥4,当且仅当k=$\frac{1}{2}$时取等号.
故△APQ的面积有最大值$4\sqrt{2}$(12分)
点评 本题考查直线与椭圆的位置关系的综合应用,椭圆的方程的求法,考查转化思想以及计算能力.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2016,+∞) | D. | (-∞,0)∪(2016,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值16 | B. | 最小值$\frac{1}{16}$ | C. | 最小值16 | D. | 最小值$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com