
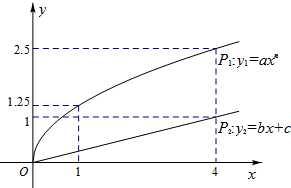
 某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品可分别获得y1,y2万元的利润,利润曲线P1,P2如图所示.问怎样分配投资额,才能使投资获得最大利润?
某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品可分别获得y1,y2万元的利润,利润曲线P1,P2如图所示.问怎样分配投资额,才能使投资获得最大利润?| 5 |
| 4 |
| x |
| 1 |
| 4 |
| 5 |
| 4 |
| x |
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
| x |
| 10 |
| 4 |
| 1 |
| 4 |
| x |
| 5 |
| 2 |
| 65 |
| 16 |
| x |
| 5 |
| 2 |
| 25 |
| 4 |
| 65 |
| 16 |


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
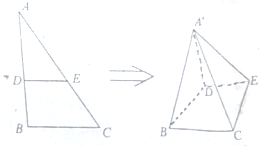 如图,在直角△ABC中,B=90°,BC=1,AB=
如图,在直角△ABC中,B=90°,BC=1,AB=| 3 |
| AD |
| AB |
| AE |
| AC |
查看答案和解析>>
科目:高中数学 来源: 题型:
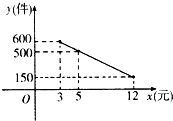 某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.
某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
 对某小区居民一个月内参加娱乐活动的次数进行统计,随机抽取M名居民作为样本,得到这M名居民参加娱乐活动的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某小区居民一个月内参加娱乐活动的次数进行统计,随机抽取M名居民作为样本,得到这M名居民参加娱乐活动的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 24 | n |
| [20,25) | m | p |
| [25,30) | 1 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com