
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:选择题
样本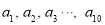 的平均数为
的平均数为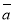 ,样本
,样本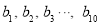 的平均数为
的平均数为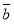 ,那么样本
,那么样本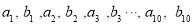 的平均数为( )
的平均数为( )
A. 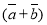 B.
B.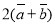 C.
C. 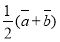 D.
D. 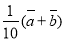
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
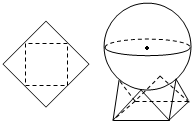 用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )| A. | $\frac{\sqrt{2}+2}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{10}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{10}-\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
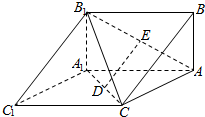 如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2$\sqrt{2}$,AA1=AC=4,∠A1C1C=60°,D、E分别为A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2$\sqrt{2}$,AA1=AC=4,∠A1C1C=60°,D、E分别为A1C,AB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
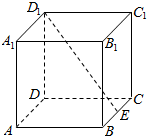 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
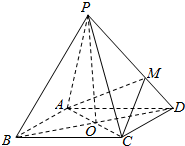 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
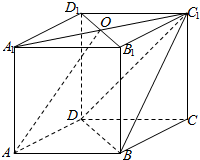 在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=1,∠BAD=60°.
在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=1,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
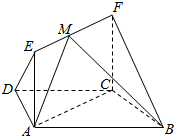 如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.
如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com