
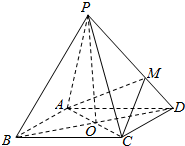
 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.分析 (1)连结OM,BN,根据线面平行的性质得出BN∥OM,故$\frac{DO}{DB}=\frac{DM}{DN}$=$\frac{1}{2}$,所以N为PD的另一个三等分点;
(2)由菱形的性质可得OC=$\frac{1}{2}$AC=1,由勾股定理求出PO,于是V棱锥A-PMC=V棱锥P-ACD-V棱锥M-ACD=$\frac{2}{3}$V棱锥P-ACD.
解答 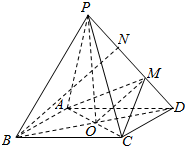 解:(1)连结OM,BN,
解:(1)连结OM,BN,
∵BN∥面AMC,BN?平面BDN,平面BDN∩平面ACM=OM,
∴BN∥OM,
∴$\frac{DO}{DB}=\frac{DM}{DN}$=$\frac{1}{2}$,
∵M是PD靠近D的三等分点,∴N是PD靠近P点的三等分点.
(2)∵底面ABCD是边长为2的菱形,∠BCD=120°,
∴AO=OC=1,△ACD是等边三角形.∴S△ACD=$\frac{\sqrt{3}}{4}A{C}^{2}$=$\sqrt{3}$.
∵PO⊥面ABCD,AC?平面ABCD,
∴PO⊥AC,∴PO=$\sqrt{P{C}^{2}-O{C}^{2}}$=$\sqrt{3}$,
∵M是靠近D点的三等分点,∴M到平面ABCD的距离h=$\frac{1}{3}$PO=$\frac{\sqrt{3}}{3}$.
∴V棱锥A-PMC=V棱锥P-ACD-V棱锥M-ACD=$\frac{1}{3}$S△ACD•PO-$\frac{1}{3}$S△ACD•$\frac{1}{3}$PO=$\frac{2\sqrt{3}}{9}$.
点评 本题考查了线面平行的性质,棱锥的体积计算,属于中档题.


科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.
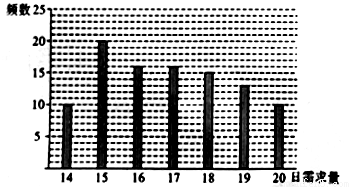
(1)求当天的利润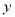 (单位:元)关于当天需求量
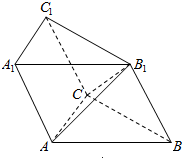
(单位:元)关于当天需求量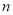 (单位:个,
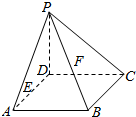
(单位:个,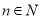 )的函数解析式;
)的函数解析式;
(2)求当天的利润不低于750元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.
如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{2}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ | D. | $\frac{x^2}{2}-\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD
已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
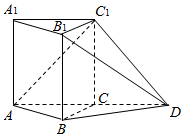 如图,在直棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=1,延长AC至D,使AC=CD,连接BD,B1D,C1D
如图,在直棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=1,延长AC至D,使AC=CD,连接BD,B1D,C1D查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com