
 已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD
已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD分析 (1)利用线面平行的判定定理即可证明EF∥平面PCD;
(2)若∠PDA=60°,利用线面垂直的性质定理即可证明EF⊥BC;
(3)若PD⊥平面ABCD,建立空间坐标系,求出平面的法向量,利用向量法即可求二面角A=PB-C的余弦值.
解答  (1)证明:取PC的中点G,连接FG,
(1)证明:取PC的中点G,连接FG,
∵E,F分别是AD,PB的中点,
∴FG为△PBC的中位线,
则FG∥BC,FG=$\frac{1}{2}$BC,DE=$\frac{1}{2}$BC,
则DE∥FG,且DE=FG,
则四边形DFGD为平行四边形,
则EF∥DG,
∵EF?平面PCD,DG?平面PCD
∴EF∥平面PCD;
(2)若∠PDA=60°,
∵PD=AD,
∴△PAD是等腰三角形,
则PE⊥AD,
∵底面ABCD为菱形且∠ADC=120°,
∴△ABD是等边三角形,
∴AE⊥BE,
∵PE∩BE=E,
∴AE⊥平面PBE,
∵BC∥AE,
∴BC⊥平面PBE,
∵EF?平面PBE
∴EF⊥BC;
(3)连接AC,BD交于O,连接OF,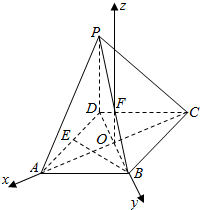
则AC⊥BD,OF∥PD
若PD⊥平面ABCD,
则OF⊥平面ABCD,
建立以O为坐标原点,OA,OB,OF为x,y,z轴的空间直角坐标系如图:
设PD=AD=2,则OB=1,OA=OC=$\sqrt{3}$,OF=1,
则A($\sqrt{3}$,0,0),C(-$\sqrt{3}$,0,0),B(0,1,0),P(0,0,2),
则$\overrightarrow{PB}$=(0,1,-2),$\overrightarrow{AB}$=(-$\sqrt{3}$,1,0),$\overrightarrow{BC}$=(-$\sqrt{3}$,-1,0),
设$\overrightarrow{m}$=(x,y,z)为面APB的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=0}\\{\overrightarrow{m}•\overrightarrow{PB}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-\sqrt{3}x+y=0}\\{y-2z=0}\end{array}\right.$,
令z=1,则y=2,x=$\frac{2}{\sqrt{3}}$,
则$\overrightarrow{m}$=($\frac{2}{\sqrt{3}}$,2,1),
设平面PBC的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=0}\\{\overrightarrow{n}•\overrightarrow{BC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{y-2z=0}\\{-\sqrt{3}x-y=0}\end{array}\right.$,
令z=1,则y=2,x=-$\frac{2}{\sqrt{3}}$,
即$\overrightarrow{n}$=(-$\frac{2}{\sqrt{3}}$,2,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-\frac{2}{\sqrt{3}}×\frac{2}{\sqrt{3}}+2×2+1×1}{\sqrt{(\frac{2}{\sqrt{3}})^{2}+{2}^{2}+{1}^{2}}•\sqrt{(-\frac{2}{\sqrt{3}})^{2}+{2}^{2}+{1}^{2}}}$=$\frac{11}{19}$,
∵二面角A-PB-C是钝二面角,
则面角A-PB-C的余弦值是-$\frac{11}{19}$.
点评 本题综合考查空间直线平行和垂直的判断以及空间角的计算,涉及二面角的平面角,利用向量法是解决空间角常用的方法,考查的知识面较广,难度中等.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
 2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),如表是易建联在这9场比赛中投篮的统计数据.
2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),如表是易建联在这9场比赛中投篮的统计数据.| 比分 | 易建联技术统计 | |||
| 投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
| 中国91-42新加坡 | 3/7 | 6/7 | 12 | 59.52% |
| 中国76-73韩国 | 7/13 | 6/8 | 20 | 60.53% |
| 中国84-67约旦 | 12/20 | 2/5 | 26 | 58.56% |
| 中国75-62哈萨克期坦 | 5/7 | 5/5 | 15 | 81.52% |
| 中国90-72黎巴嫩 | 7/11 | 5/5 | 19 | 71.97% |
| 中国85-69卡塔尔 | 4/10 | 4/4 | 13 | 55.27% |
| 中国104-58印度 | 8/12 | 5/5 | 21 | 73.94% |
| 中国70-57伊朗 | 5/10 | 2/4 | 13 | 55.27% |
| 中国78-67菲律宾 | 4/14 | 3/6 | 11 | 33.05% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
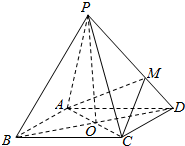 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
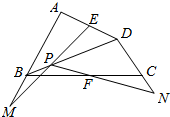 如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.
如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
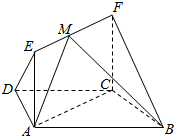 如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.
如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com