练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知点A（4，1，3），B（6，3，2），且$\overrightarrow{AC}=3\overrightarrow{AB}$，则点C的坐标为（10，7，0）．

    分析 设出C的坐标，根据条件列出方程解出．

    解答 解：设C（a，b，c），则$\overrightarrow{AC}$=（a-4，b-1，c-3），$\overrightarrow{AB}$=（2，2，-1）．
    ∵$\overrightarrow{AC}=3\overrightarrow{AB}$，∴$\left\{\begin{array}{l}{a-4=6}\\{b-1=6}\\{c-3=-3}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=10}\\{b=7}\\{c=0}\end{array}\right.$．
    故答案为（10，7，0）．

    点评 本题考查了空间向量的坐标运算，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届重庆市高三文上适应性考试一数学试卷（解析版） 题型：解答题

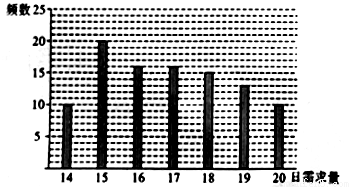
    某蛋糕店每天制作生日蛋糕若干个，每个生日蛋糕的成本为50元，然后以每个100元的价格出售，如果当天卖不完，剩下的蛋糕作垃圾处理．现需决策此蛋糕店每天应该制作几个生日蛋糕，为此搜集并整理了100天生日蛋糕的日需求量（单位：个），得到如图所示的柱状图，以100天记录的各需求量的频率作为每天各需求量发生的概率．若蛋糕店一天制作17个生日蛋糕．

    （1）求当天的利润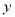（单位：元）关于当天需求量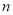（单位：个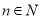，）的函数解析式；

    （2）求当天的利润不低于750元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知边长为3的正三角形ABC的三个顶点都在半径为2的球O的球面上，则点O到平面ABC的距离为（　　）
    A．1B．$\frac{\sqrt{2}}{2}$C．$\sqrt{2}$D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

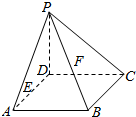    10．已知在四棱锥P-ABCD中，底面ABCD为菱形且∠ADC=120°，E，F分别是AD，PB的中点且PD=AD
    （1）求证：EF∥平面PCD；
    （2）若∠PDA=60°，求证：EF⊥BC；
    （3）若PD⊥平面ABCD，求二面角A=PB-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

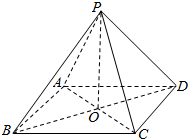    17．已知P是四边形ABCD所在平面外一点，PA=PB=PD，在四边形ABCD中，BA=AD，BA⊥AD，O是BD的中点，OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP．
    （1）求证：PD⊥AC；
    （2）求二面角A-PD-C余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知圆（x-2）2+y2=4，则过抛物线y2=4x的焦点的直线与已知圆相交的最短弦长等于$2\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．函数f（x）在x=x0处导数存在，若p：f′（x0）=0；q：x=x0是f（x）的极值点，则p是q的（　　）
    A．充分不必要条件B．充要条件
    C．必要不充条件D．既非充分条件也非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

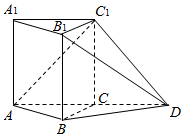    11．如图，在直棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=AA1=1，延长AC至D，使AC=CD，连接BD，B1D，C1D
    （1）求证：AC1⊥B1D；
    （2）求六面体BB1-A1ADC1的体积；
    （3）求平面B1C1D与平面ABC所成锐二面角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．等比数列{an}的各项均为正数，且2a1+3a2=1，a32=9a2a6．
    （1）求数列{an}的通项公式；
    （2）设bn+1=2log3$\frac{1}{{a}_{n}}$，求数列{anbn}的前n项和Sn．

    查看答案和解析>>

    同步练习册答案