
分析 (1)利用等比中项及a32=9a2a6可知a32=9a42,进而可得q=$\frac{1}{3}$,利用2a1+3a2=1可知a1=$\frac{1}{3}$,进而计算可得结论;
(2)通过(1)可知bn=2n-1,进而利用错位相减法计算即得结论.
解答 (本小题满分12分)
解:(1)由a32=9a2a6得:a32=9a42,即q2=$\frac{1}{9}$,
∵q>0,∴q=$\frac{1}{3}$,
又2a1+3a2=1,∴a1=$\frac{1}{3}$ …(3分)
∴an=($\frac{1}{3}$)n,…(6分)
(2)由bn+1=2log3$\frac{1}{{a}_{n}}$得:bn=2n-1,
令cn=anbn=(2n-1)•($\frac{1}{3}$)n…(8分)
∴Sn=1×$\frac{1}{3}$+3×($\frac{1}{3}$)2+5×($\frac{1}{3}$)3+…+(2n-3)×($\frac{1}{3}$)n-1+(2n-1)×($\frac{1}{3}$)n…①
$\frac{1}{3}$Sn=1×($\frac{1}{3}$)2+3×($\frac{1}{3}$)3+5×($\frac{1}{3}$)4+…+(2n-3)×($\frac{1}{3}$)n+(2n-1)×($\frac{1}{3}$)n+1…②
①-②得:$\frac{2}{3}$Sn=1×$\frac{1}{3}$+2[($\frac{1}{3}$)2+($\frac{1}{3}$)3+…+($\frac{1}{3}$)n-1+($\frac{1}{3}$)n]-(2n-1)×($\frac{1}{3}$)n+1
=$\frac{1}{3}$+2×$\frac{\frac{1}{{3}^{2}}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}$-(2n-1)×($\frac{1}{3}$)n+1,
∴Sn=1-$\frac{n+1}{3n}$…(12分)
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
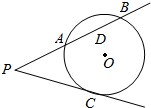 如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.
如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
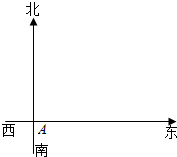 一辆消防车从A地去B地执行任务.先从A地向北偏东30°方向行驶2千米到D地.然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地.
一辆消防车从A地去B地执行任务.先从A地向北偏东30°方向行驶2千米到D地.然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com