Question

19．一辆消防车从A地去B地执行任务．先从A地向北偏东30°方向行驶2千米到D地．然后从D地沿北偏东60°方向行驶6千米到达C地，从C地又向南偏西30°方向行驶2千米才到达B地．
（1）在如图所示的坐标系中画出$\overrightarrow{AD}$，$\overrightarrow{DC}$，$\overrightarrow{CB}$，$\overrightarrow{AB}$；
（2）求B地相对于A地的位置向量．

Answer 1

分析 （1）根据题目中的方位依次作出$\overrightarrow{AD}$，$\overrightarrow{DC}$，$\overrightarrow{CB}$，$\overrightarrow{AB}$；
（2）根据方位角和距离可判断ABCD是平行四边形，求出$\overrightarrow{AB}$的方向和模长即可．

解答 解：（1）作出向量如图所示：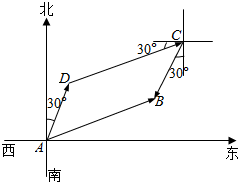

（2）∵D在A北偏东30°方向上，B在C南偏西30方向上，∴AD∥BC，
∵AD=BC=2，∴四边形ABCD是平行四边形，∴AB=DC=6，
∵C在D北偏东60°方向上，∴B在A北偏东60°方向6千米处．
∴$\overrightarrow{AB}$的方向为北偏东60°，|$\overrightarrow{AB}$|=6．

点评 本题考查了平面向量的作法和向量的几何意义，属于基础题．