
分析 (1)根据条件转化为一元二次方程的关系,利用根与系数之间的关系进行求解即可.
(2)根据充分条件和必要条件的条件进行求解即可.
解答 解:(1)若A={x|-1≤x≤4},则方程x2+ax+b=0的两根为-1和4.…(2分)
由根与系数的关系,得$\left\{\begin{array}{l}{-1+4=-a}\\{-1×4=b}\end{array}\right.$,解得a=-3,b=-4,所以a+b=-7.…(4分)
(2)由x2-2mx+m2-4<0得m-2<x<m+2,即q:m-2<x<m+2,…(6分)
¬q:x≥m+2或x≤m-2,…(8分)
因为¬q是p的必要条件,所以A⊆C.…(10分)
故m-2≥4或m+2≤-1.解得m≥6,或m≤-3.
故实数m的取值范围是(-∞,-3]∪[6,+∞).…(12分)
点评 本题主要考查充分条件和必要条件以及集合关系的应用,根据条件建立方程或不等式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
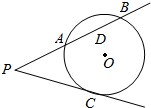 如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.
如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一辆消防车从A地去B地执行任务.先从A地向北偏东30°方向行驶2千米到D地.然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地.
一辆消防车从A地去B地执行任务.先从A地向北偏东30°方向行驶2千米到D地.然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com