
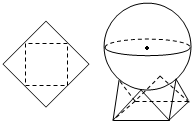
 用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )| A. | $\frac{\sqrt{2}+2}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{10}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{10}-\sqrt{2}}{2}$ |
分析 蛋槽的边长是原来硬纸板的对角线长度的一半,为$\sqrt{2}$cm,蛋槽立起来的小三角形部分高度是$\frac{\sqrt{2}}{2}$cm,由此能求出球体球心与蛋巢底面的距离.
解答 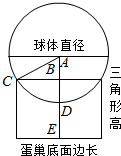 解:蛋槽的边长是原来硬纸板的对角线长度的一半,为$\sqrt{2}$cm,
解:蛋槽的边长是原来硬纸板的对角线长度的一半,为$\sqrt{2}$cm,
蛋槽立起来的小三角形部分高度是$\frac{\sqrt{2}}{2}$,
半径为$\sqrt{2}$的球体放置于蛋巢上,得到r=$\sqrt{2}$cm,
直径D=2$\sqrt{2}$cm,大于折好的蛋巢边长$\sqrt{2}$cm,
四个三角形的顶点所在的平面在鸡蛋表面所截取的小圆直径就是蛋槽的边长$\sqrt{2}$cm,
根据图示,AB段由三角形AB求出得:AB=$\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{6}}{2}$,
AE=AB+BE=$\frac{\sqrt{6}}{2}$+$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
∴球体球心与蛋巢底面的距离为$\frac{\sqrt{6}+\sqrt{2}}{2}$.
故选:B.
点评 本题考查点、线、面间距离的计算,解题时要认真审题,注意挖掘题设中的隐含条件,合理地化空间问题为平面问题,注意数形结合法的合理运用.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -2$\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
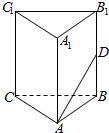 如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求:
如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
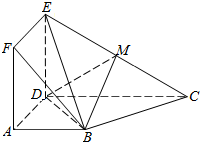 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.
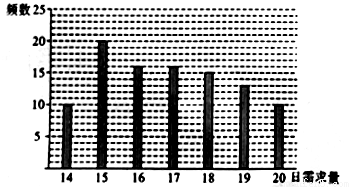
(1)求当天的利润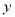 (单位:元)关于当天需求量
(单位:元)关于当天需求量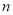 (单位:个,
(单位:个,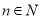 )的函数解析式;
)的函数解析式;
(2)求当天的利润不低于750元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
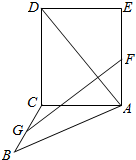 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
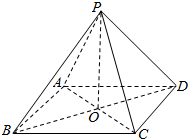 已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.
已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com