
分析 求关系式的倒数,得到新数列是等差数列,然后求解通项公式,求解即可.
解答 解:数列{an}中,a1=2,an+1=$\frac{{a}_{n}}{{a}_{n}+1}$,
可得$\frac{1}{{a}_{n+1}}=1+\frac{1}{{a}_{n}}$,所以{$\frac{1}{{a}_{n}}$}是以$\frac{1}{2}$为首项,1为公差的等差数列,
所以$\frac{1}{{a}_{n}}=\frac{1}{2}+n-1$,
可得an=$\frac{2}{2n-1}$,
则a2017=$\frac{2}{4033}$.
故答案为:$\frac{2}{4033}$.
点评 本题考查数列的递推关系式的应用,数列的通项公式的求法,考查计算能力.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1,2} | B. | {-2,-1} | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
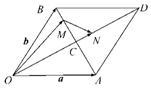 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 常喝 | 不常喝 | 总计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 总计 | 30 |
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com