
分析 由双曲线方程求出渐近线方程判断①;求出函数f(x)=lgx-$\frac{1}{x}$的零点所在的区间判断②;由线性回归直线方程的意义判断③;由已知求出P(X<-1)的值判断④.
解答 解:①由$\frac{{y}^{2}}{2}$-x2=1,得a2=2,b2=1,∴a=$\sqrt{2},b=1$,则双曲线的渐近线方程为y=$±\frac{a}{b}x$=±$\sqrt{2}$x,故①正确;
②函数f(x)=lgx-$\frac{1}{x}$为(0,+∞)上的增函数,又f(1)=-1<0,f(10)=1-$\frac{1}{10}=\frac{9}{10}$>0,则零点所在的区间是(1,10),故②正确;
③线性回归方程为$\stackrel{∧}{y}$=3+2x,当变量x增加2个单位,其预报值平均增加4个单位,正确;
④随机变量X服从正态分布N(0,1),且P(-1≤X≤1)=m,则P(X<-1)=$\frac{1-m}{2}$,故④错误.
∴正确命题的序号是①②③.
故答案为:①②③.
点评 本题考查命题的真假判断与应用,考查双曲线的性质,考查函数零点判定定理的应用,训练了正态分布概率的求法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 54cm2 | B. | 24cm2 | C. | 18cm2 | D. | 12cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 观察如图所示的正方形图案,每条边(包括两个端点)有n(n≥2,n∈N*)个圆点,第n个图案中圆点的总数是Sn.按此规律推断出Sn与n的关系式为( )
观察如图所示的正方形图案,每条边(包括两个端点)有n(n≥2,n∈N*)个圆点,第n个图案中圆点的总数是Sn.按此规律推断出Sn与n的关系式为( )| A. | Sn=2n | B. | Sn=4n | C. | Sn=2n | D. | Sn=4n-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b中至少有一个为0 | B. | a,b中至少有一个不为0 | ||
| C. | a,b全为0 | D. | a,b中只有一个不为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
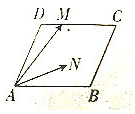 如图,在平行四边形ABCD中,AB=4,AD=2,∠DAB=60°,点M在线段DC上,且满足$\overrightarrow{DM}$=$\frac{1}{4}$$\overrightarrow{DC}$,若N是平行四边形ABCD内的任意一点(含边界),则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是[0,13].
如图,在平行四边形ABCD中,AB=4,AD=2,∠DAB=60°,点M在线段DC上,且满足$\overrightarrow{DM}$=$\frac{1}{4}$$\overrightarrow{DC}$,若N是平行四边形ABCD内的任意一点(含边界),则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是[0,13].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | [4,+∞) | C. | (-∞,2] | D. | (0,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com