
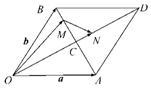
 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$. 分析 根据向量的三角形法则和平行四边形法则以及向量的数乘运算即可求出
解答 解:$\overrightarrow{OM}$=$\overrightarrow{OA}$+$\overrightarrow{AM}$=$\overrightarrow{OA}$+$\frac{5}{6}$$\overrightarrow{AB}$=$\overrightarrow{OA}$+$\frac{5}{6}$($\overrightarrow{OB}$-$\overrightarrow{OA}$)=$\frac{1}{6}$$\overrightarrow{a}$+$\frac{5}{6}$$\overrightarrow{b}$,
$\overrightarrow{ON}$=$\frac{2}{3}$$\overrightarrow{OD}$=$\frac{2}{3}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$,
∴$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$=$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{6}$$\overrightarrow{b}$
点评 本题考查了向量的三角形法则和平行四边形法则以及向量的数乘运算,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 54cm2 | B. | 24cm2 | C. | 18cm2 | D. | 12cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 观察如图所示的正方形图案,每条边(包括两个端点)有n(n≥2,n∈N*)个圆点,第n个图案中圆点的总数是Sn.按此规律推断出Sn与n的关系式为( )
观察如图所示的正方形图案,每条边(包括两个端点)有n(n≥2,n∈N*)个圆点,第n个图案中圆点的总数是Sn.按此规律推断出Sn与n的关系式为( )| A. | Sn=2n | B. | Sn=4n | C. | Sn=2n | D. | Sn=4n-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com