
【题目】已知定义在R上的函数f(x)= ![]() (a∈R)是奇函数,函数g(x)=
(a∈R)是奇函数,函数g(x)= ![]() 的定义域为(﹣1,+∞).
的定义域为(﹣1,+∞).
(1)求a的值;
(2)若g(x)= ![]() 在(﹣1,+∞)上递减,根据单调性的定义求实数m的取值范围;
在(﹣1,+∞)上递减,根据单调性的定义求实数m的取值范围;
(3)在(2)的条件下,若函数h(x)=f(x)+g(x)在区间(﹣1,1)上有且仅有两个不同的零点,求实数m的取值范围.
【答案】
(1)解:∵函数 ![]() 是奇函数,
是奇函数,
∴f(﹣x)=﹣f(x),
∴ ![]() 得a=0
得a=0
(2)解:∵ ![]() 在(﹣1,+∞)上递减,
在(﹣1,+∞)上递减,
∴任给实数x1,x2,当﹣1<x1<x2时,g(x1)>g(x2),
∴ ![]() ,
,
∴m<0
(3)解:由(1)得 ![]() ,
,
令h(x)=0,即 ![]() ,
,
化简得x(mx2+x+m+1)=0,
∴x=0或 mx2+x+m+1=0,
若0是方程mx2+x+m+1=0的根,则m=﹣1,
此时方程mx2+x+m+1=0的另一根为1,不符合题意,
∴函数h(x)=f(x)+g(x)在区间(﹣1,1)上有且仅有两个不同的零点,
等价于方程mx2+x+m+1=0(※)在区间(﹣1,1)上有且仅有一个非零的实根,
①当△=12﹣4m(m+1)=0时,得 ![]() ,
,
若 ![]() ,则方程(※)的根为
,则方程(※)的根为 ![]() ,符合题意;
,符合题意;
若 ![]() ,则与(2)条件下m<0矛盾,不符合题意,
,则与(2)条件下m<0矛盾,不符合题意,
∴ ![]() ,
,
②当△>0时,令h(x)=mx2+x+m+1,
由 ![]() ,得﹣1<m<0,
,得﹣1<m<0,
综上所述,所求实数m的取值范围是 ![]()
【解析】(1)根据函数的奇偶性,求出a的值即可;(2)根据单调性的定义判断m的范围即可;(3)根据根域系数的关系,通过讨论△的符号,求出m的范围即可.
【考点精析】本题主要考查了函数单调性的性质和函数奇偶性的性质的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】甲、乙两支球队进行总决赛,比赛采用七场四胜制,即若有一队先胜四场,则此队为总冠军,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为![]() .据以往资料统计,第一场比赛可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.
.据以往资料统计,第一场比赛可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.
(I)求总决赛中获得门票总收入恰好为300万元的概率;
(II)设总决赛中获得门票总收入为X,求X的均值E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°. 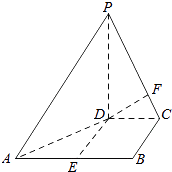
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)是偶函数,且在(﹣∞,0]上是增函数,又f(2)=0,则xf(x)>0的解集是( )
A.(﹣2,2)
B.(﹣∞,﹣2)∪(0,2)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣2,0]∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出假设H:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算的K2≈3.918,经查临界值表知P(K2≥3.841)≈0.05.则下列表述中正确的是( )
A.有95℅的把握认为“这种血清能起到预防感冒的作用”
B.若有人未使用该血清,那么他一年中有95℅的可能性得感冒
C.这种血清预防感冒的有效率为95℅
D.这种血清预防感冒的有效率为5℅
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD,E分别为AP的中点.
(Ⅰ)求证:DE垂直于平面PAB;
(Ⅱ)设BC =![]() ,AB=2,求直线EB与平面ABD所成的角的大小.
,AB=2,求直线EB与平面ABD所成的角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为函数f(x)的不动点.已知f(x)=x2+bx+c
(1)若f(x)有两个不动点为﹣3,2,求函数y=f(x)的零点?
(2)若c= ![]() 时,函数f(x)没有不动点,求实数b的取值范围?
时,函数f(x)没有不动点,求实数b的取值范围?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com