
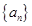 的前n项和为
的前n项和为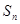 ,首项
,首项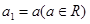 ,公差
,公差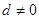 ,且
,且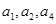 成等比数列。
成等比数列。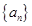 的通项公式及
的通项公式及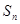 ;
; 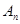 =
=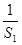 +
+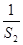 +
+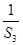 +…+
+…+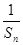 ,
, 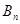 =
=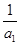 +
+ 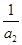 +
+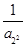 +… +
+… +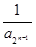 ,
,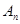 与
与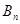 的大小。
的大小。科目:高中数学 来源:不详 题型:解答题
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式.
,求Tn的表达式.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 、…、
、…、
 是曲线
是曲线 :
: 上的
上的 个点,点
个点,点 (
( )在
)在 轴的正半轴上,且
轴的正半轴上,且 是正三角形(
是正三角形( 是坐标原点).
是坐标原点). 、
、 、
、 ;
; (
( )的横坐标
)的横坐标 关于
关于 的表达式并证明.
的表达式并证明.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
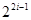 ( i≥1).
( i≥1).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
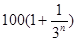 万元.
万元.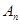 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为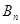 万元(须扣除开发所投入资金),求
万元(须扣除开发所投入资金),求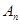 ,
,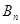 的表达式.
的表达式.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
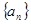 (
(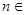 N+)中,
N+)中,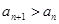 ,
,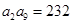 ,
,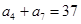 .
. 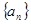 的通项公式;
的通项公式;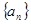 的项重新组合,得到新数列
的项重新组合,得到新数列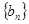 ,具体方法如下:
,具体方法如下: 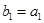 ,
,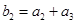 ,
,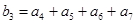 ,
,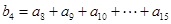 ,…,依此类推,
,…,依此类推,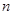 项
项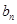 由相应的
由相应的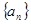 中
中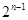 项的和组成,求数列
项的和组成,求数列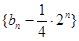 的前
的前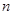 项和
项和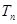 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com